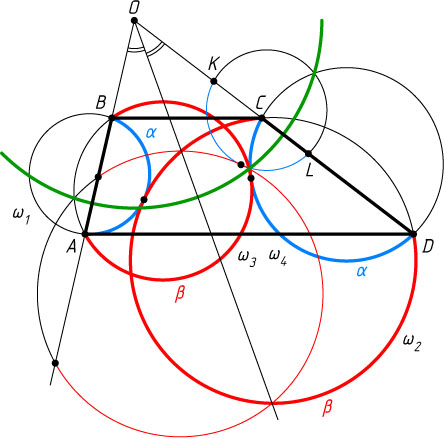
2351. Боковые стороны AB
и CD
трапеции ABCD
являются соответственно хордами окружностей \omega_{1}
и \omega_{2}
, касающихся друг друга внешним образом. Градусные меры касающихся дуг AB
и CD
равны \alpha
и \beta
. Окружности \omega_{3}
и \omega_{4}
также имеют хорды AB
и CD
соответственно. Их дуги AB
и CD
, расположенные с той же стороны от хорд, что соответствующие дуги первых двух окружностей, имеют градусные меры \beta
и \alpha
. Докажите, что \omega_{3}
и \omega_{4}
тоже касаются.
Решение. Пусть O
— точка пересечения прямых AB
и CD
, \Omega_{1}
и \Omega_{2}
— окружности, симметричные соответственно \omega_{1}
и \omega_{2}
относительно биссектрисы угла AOD
. Рассмотрим окружности \Omega_{4}
и \Omega_{3}
, полученные из соответственно \Omega_{1}
и \Omega_{2}
инверсией относительно окружности с центром O
и радиусом R=\sqrt{OA\cdot OC}=\sqrt{OB\cdot OD}
. Они, очевидно, касаются.
Заметим, что при этом \Omega_{4}
проходит через точки C
и D
. Действительно, если K
и L
— точки симметричные точкам соответственно B
и A
относительно биссектрисы угла AOD
, то OK=OB
и OL=OA
, поэтому OK\cdot OD=OB\cdot OD=R^{2}
и OL\cdot OC=OA\cdot OC=R^{2}
. Значит, при рассматриваемой инверсии точка K
переходит в D
, а точка L
— в C
.
В то же время, окружность \Omega_{4}
может быть получена из \Omega_{1}
не только инверсией, но и гомотетией с центром O
и коэффициентом \frac{OD}{OL}=\frac{OD}{OA}=\frac{OC}{OB}=\frac{OC}{OK}
. Поэтому градусная мера дуги CD
в \Omega_{4}
равна \alpha
. Следовательно, \Omega_{4}
совпадает с \omega_{4}
. Аналогично, \Omega_{3}
совпадает с \omega_{3}
.
Автор: Ивлев Ф. А.
Источник: Турнир городов. — 2010-2011, XXXII, весенний тур, старшие классы, основной вариант