2551. Отрезки AA_{1}
, BB_{1}
и CC_{1}
— высоты треугольника ABC
. Найдите углы этого треугольника, если известно, что он подобен треугольнику A_{1}B_{1}C_{1}
.
Ответ. 60^{\circ}
, 60^{\circ}
, 60^{\circ}
или \frac{180^{\circ}}{7}
, \frac{360^{\circ}}{7}
, \frac{720^{\circ}}{7}
.
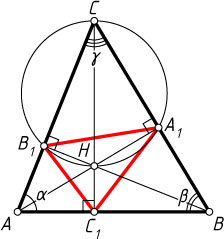
Решение. Предположим, что треугольник ABC
— остроугольный. Пусть его углы при вершинах A
, B
и C
равны \alpha
, \beta
и \gamma
соответственно, причём \alpha\geqslant\beta\geqslant\gamma
, а высоты AA_{1}
, BB_{1}
и CC_{1}
пересекаются в точке H
(рис. 1).
Из точек A_{1}
и B_{1}
отрезок CH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CH
. Вписанные в эту окружность углы HA_{1}B_{1}
и HCB_{1}
опираются на одну и ту же дугу, поэтому
\angle HA_{1}B_{1}=\angle HCB_{1}=90^{\circ}-\angle CAC_{1}=90^{\circ}-\alpha.
Аналогично, \angle HA_{1}C_{1}=90^{\circ}-\alpha
, следовательно,
\angle B_{1}A_{1}C_{1}=\angle HA_{1}B_{1}+\angle HA_{1}C_{1}=90^{\circ}-\alpha+90^{\circ}-\alpha=180^{\circ}-2\alpha.
Аналогично,
\angle A_{1}B_{1}C_{1}=180^{\circ}-2\beta,~\angle A_{1}C_{1}B_{1}=180^{\circ}-2\gamma,
а так как \alpha\geqslant\beta\geqslant\gamma
, то 180^{\circ}-2\gamma\geqslant180^{\circ}-2\beta\geqslant180^{\circ}-2\alpha
, то
180^{\circ}-2\gamma=\alpha,~180^{\circ}-2\beta=\beta,~180^{\circ}-2\alpha=\gamma,
откуда находим, что \alpha=\beta=\gamma=60^{\circ}
, т. е. треугольник ABC
— равносторонний.
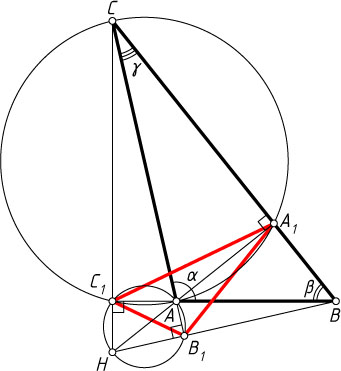
Предположим, что один из углов треугольника ABC
— тупой, \angle A=\alpha
, \angle B=\beta
, \angle C=\gamma
, причём \alpha\gt\beta\geqslant\gamma
, H
— точка пересечения высот (рис. 2).
Точки B_{1}
и C_{1}
лежат на окружности с диаметром AH
, поэтому
\angle B_{1}HC_{1}=180^{\circ}-\angle B_{1}AC_{1}=180^{\circ}-\alpha.
Точки A_{1}
и C_{1}
лежат на окружности с диаметром AC
, поэтому
\angle AA_{1}C_{1}=\angle ACC_{1}=\angle ABB_{1}=90^{\circ}-\angle B_{1}HC_{1}=90^{\circ}-(180^{\circ}-\alpha)=\alpha-90^{\circ}.
Аналогично, \angle AA_{1}B_{1}=\alpha-90^{\circ}
. Следовательно,
\angle B_{1}A_{1}C_{1}=\angle AA_{1}C_{1}+\angle AA_{1}B_{1}=(\alpha-90^{\circ})+(\alpha-90^{\circ})=2\alpha-180^{\circ}.
Кроме того,
\angle AC_{1}A_{1}=\angle ACA_{1}=\gamma,~
\angle AC_{1}B_{1}=\angle AHB_{1}=90^{\circ}-\angle HBA_{1}=90^{\circ}-(\alpha-90^{\circ})-\beta=180^{\circ}-\alpha-\beta=\gamma,
следовательно,
\angle A_{1}C_{1}B_{1}=\angle AC_{1}A_{1}+\angle AC_{1}B_{1}=\gamma+\gamma=2\gamma.
Аналогично докажем, что \angle A_{1}B_{1}C_{1}=2\beta
.
Предположим, что наибольший угол треугольника A_{1}B_{1}C_{1}
равен 2\alpha-180^{\circ}
. Тогда 2\alpha-180^{\circ}=\alpha
, т. е. \alpha=180^{\circ}
, что невозможно.
Пусть наибольший угол треугольника ABC
равен 2\beta
, а наименьший равен 2\gamma
. Тогда
2\beta=\alpha,~2\alpha-180^{\circ}=\beta,~2\gamma=\gamma,
что также невозможно, так как \gamma\ne0
.
Остаётся случай, когда наибольший угол треугольника A_{1}B_{1}C_{1}
равен 2\beta
, а наименьший равен 2\alpha-180^{\circ}
. Тогда
2\beta=\alpha,~2\gamma=\beta,~2\alpha-180^{\circ}=\gamma.
Из этой системы находим, что
\gamma=\frac{180^{\circ}}{7},~\beta=\frac{360^{\circ}}{7},~\alpha=\frac{720^{\circ}}{7}.
Примечание. См. также статью А.Егорова «Ортоцентрический треугольник», Квант, 2001, N4, с.36-38.

