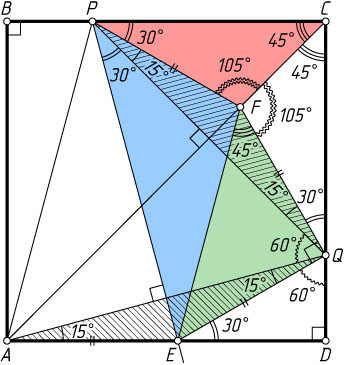
2555. Точки P
и Q
лежат на сторонах соответственно BC
и CD
квадрата ABCD
, причём треугольник APQ
— равносторонний. Прямая, проходящая через точку P
перпендикулярно стороне AQ
, пересекает AD
в точке E
. Точка F
расположена вне треугольника APQ
, причём треугольники PQF
и AQE
равны. Докажите, что FE=2FC
.
Решение. Прямая PE
— серединный перпендикуляр к отрезку AQ
, поэтому EA=EQ
, значит, треугольники AQE
и PQF
— равнобедренные. Из равенства прямоугольных треугольников ADQ
и ABP
(по катету и гипотенузе) следует равенство углов DAQ
и BAP
, значит, каждый из этих углов равен 15^{\circ}
, т. е. углы при основаниях равнобедренных треугольников AQE
и PQF
равны по 15^{\circ}
.
Точки A
и C
равноудалены от концов отрезка PQ
, значит, прямая AC
— серединный перпендикуляр к отрезку PQ
, а так как FP=FQ
, то точка F
лежит на AC
.
Треугольник CPQ
— прямоугольный и равнобедренный, поэтому
\angle CPQ=\angle CQP=45^{\circ},~
\angle CPF=\angle CPQ-\angle QPF=45^{\circ}-15^{\circ}=30^{\circ},
\angle CFP=180^{\circ}-45^{\circ}-30^{\circ}=105^{\circ},~\angle CQF=\angle CPF=30^{\circ},~
\angle DEQ=\angle DAQ+\angle AQE=15^{\circ}+15^{\circ}=30^{\circ},~
\angle DQE=90^{\circ}-\angle DEQ=90^{\circ}-30^{\circ}=60^{\circ},~
\angle EQF=180^{\circ}-\angle CQF-\angle DQE=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ},
а так как QF=QE
, то треугольник EQF
— также прямоугольный и равнобедренный, значит,
\angle EFQ=45^{\circ},~\angle PFE=360^{\circ}-\angle PFC-\angle QFC-\angle EFQ=
=360^{\circ}-105^{\circ}-105^{\circ}-45^{\circ}=105^{\circ},
а так как
\angle EPF=\angle EPQ+\angle QPE=30^{\circ}+15^{\circ}=45^{\circ},
то треугольник EFP
подобен треугольнику PFC
по двум углам, причём коэффициент подобия равен \frac{FE}{PE}=\frac{FE}{FQ}=\sqrt{2}
, значит, \frac{PE}{FC}=\frac{FE}{PE}=\sqrt{2}
. Следовательно,
\frac{FE}{FC}=\frac{FE}{PE}\cdot\frac{PE}{FC}=\sqrt{2}\cdot\sqrt{2}=2,
что и требовалось доказать.