2812. Две окружности, радиусы которых относятся как 9-4\sqrt{3}
, касаются друг друга внутренним образом. Проведены две хорды большей окружности, равные по длине и касающиеся меньшей окружности. Одна из этих хорд перпендикулярна отрезку, соединяющему центры окружностей, а другая нет. Найдите угол между этими хордами.
Ответ. 30^{\circ}
.
Указание. Равные хорды окружности равноудалены от её центра.
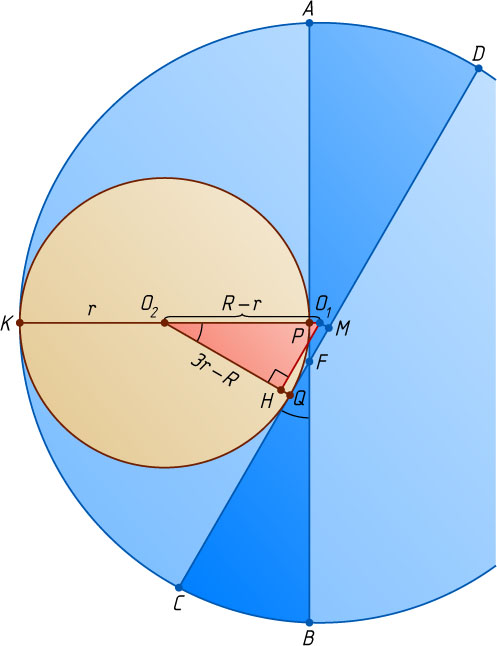
Решение. Пусть окружности радиусов R\gt r
с центрами O_{1}
и O_{2}
соответственно касаются внутренним образом в точке K
, хорда AB
большей окружности перпендикулярна O_{1}O_{2}
и касается меньшей окружности в точке P
, а равная ей хорда CD
большей окружности касается меньшей окружности в точке Q
и пересекается с хордой AB
в точке F
. Опустим перпендикуляр O_{1}M
на CD
и рассмотрим прямоугольную трапецию O_{1}O_{2}QM
.
Поскольку равные хорды окружности равноудалены от её центра, то
O_{1}M=O_{1}P=O_{1}K-PK=R-2r.
Опустим перпендикуляр O_{1}H
на O_{2}Q
. Тогда
O_{2}H=O_{2}Q-HQ=O_{2}Q-O_{1}M=r-(R-2r)=3r-R,
значит,
\cos\angle O_{1}O_{2}H=\frac{O_{2}H}{O_{1}O_{2}}=\frac{3r-R}{R-r}=\frac{3-\frac{R}{r}}{\frac{R}{r}-1}=\frac{3-(9-4\sqrt{3})}{9-4\sqrt{3}-1}=
=\frac{4\sqrt{3}-6}{8-4\sqrt{3}}=\frac{2\sqrt{3}-3}{4-2\sqrt{3}}=\frac{1}{2}\cdot\frac{\sqrt{3}(2-\sqrt{3})}{2-\sqrt{3}}=\frac{\sqrt{3}}{2}.
Следовательно,
\angle QFB=\angle O_{1}O_{2}H=30^{\circ}.
Заметим, что
\sqrt{3}\lt2\Leftrightarrow3\lt2\sqrt{3}\Leftrightarrow6\lt4\sqrt{3}\Leftrightarrow9-4\sqrt{3}\lt3,
поэтому \frac{R}{r}=9-4\sqrt{3}\lt3
. Это означает, что точка H
действительно лежит на отрезке O_{2}Q
.