2898. Длины сторон треугольника различны и образуют арифметическую прогрессию. Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна одной из сторон треугольника.
Решение. Если числа образуют арифметическую прогрессию, то одно из них есть среднее арифметическое двух других. Пусть O
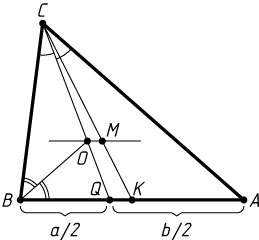
— центр вписанной окружности (точка пересечения биссектрис) треугольника ABC
, в котором AC=b
, BC=a
, AB=\frac{a+b}{2}
. Тогда, если CQ
— биссектриса треугольника ABC
, то \frac{BQ}{AQ}=\frac{BC}{AC}=\frac{a}{b}
, значит, BQ=\frac{a}{2}
и AQ=\frac{b}{2}
, а так как BO
— биссектриса треугольника BCQ
, то \frac{CO}{OQ}=\frac{a}{\frac{a}{2}}=2
.
С другой стороны, если K
— середина стороны AB
, а M
— точка пересечения медиан треугольника ABC
, то \frac{CM}{MK}=2
. Поэтому \frac{CO}{OQ}=\frac{CM}{MK}
, значит, OM\parallel AB
. Что и требовалось доказать.
Примечание. Верно и обратное: если OM\parallel AB
, то c=\frac{a+b}{2}
.
Действительно, по свойству биссектрисы треугольника
\frac{BC}{BQ}=\frac{CO}{OQ}=\frac{CM}{MK}=\frac{2}{1},
поэтому BQ=\frac{1}{2}BC=\frac{a}{2}
. Аналогично AQ=\frac{b}{2}
. Следовательно, AB=\frac{a+b}{2}
.
