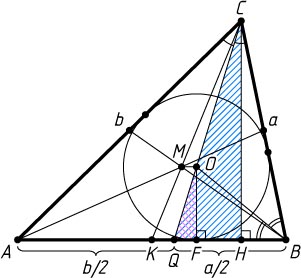
2899. Длины сторон треугольника образуют арифметическую прогрессию. Докажите, что радиус вписанной окружности равен трети одной из высот треугольника.
Решение. Если числа образуют арифметическую прогрессию, то одно из них есть среднее арифметическое двух других. Пусть O
— центр вписанной окружности (точка пересечения биссектрис) треугольника ABC
, в котором AC=b
, BC=a
, AB=\frac{a+b}{2}
. Тогда, если CQ
— биссектриса треугольника ABC
, то \frac{BQ}{AQ}=\frac{BC}{AC}=\frac{a}{b}
, значит, BQ=\frac{a}{2}
и AQ=\frac{b}{2}
, а так как BO
— биссектриса треугольника BCQ
, то \frac{CO}{OQ}=\frac{a}{\frac{a}{2}}=2
.
С другой стороны, если K
— середина стороны AB
, а M
— точка пересечения медиан треугольника ABC
, то \frac{CM}{MK}=2
. Поэтому \frac{CO}{OQ}=\frac{CM}{MK}
, значит, OM\parallel AB
.
Пусть CH
— высота треугольника ABC
, а F
— точка касания вписанной окружности этого треугольника со стороной AB
. Тогда OF
— радиус окружности, OF\perp AB
, OF\parallel CH
. Прямоугольные треугольники QOF
и QCH
подобны, причём коэффициент подобия равен \frac{QO}{QC}=\frac{1}{3}
. Следовательно, OF=\frac{1}{3}CH
. Что и требовалось доказать.