2924. Три окружности с центрами A
, B
и C
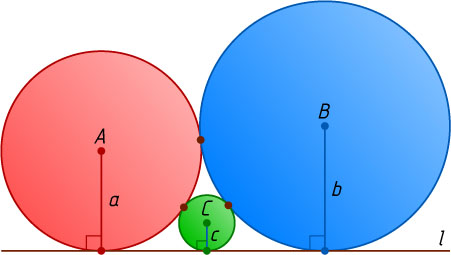
, касающиеся друг друга и прямой l
, расположены так, как показано на рисунке. Пусть a
, b
и c
— радиусы окружностей с центрами A
, B
и C
соответственно. Докажите, что \frac{1}{\sqrt{c}}=\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{b}}
.
Решение. Пусть M
, N
и K
— точки касания с прямой l
окружностей с центрами A
, B
и C
соответственно.
Поскольку линия центров касающихся окружностей проходит через точку их касания, расстояние между центрами A
и C
равно сумме радиусов этих окружностей, т. е. AC=a+c
. Пусть F
— проекция точки C
на радиус AM
окружности с центром A
, проведённый в точку касания с прямой l
. Тогда четырёхугольник CKMF
— прямоугольник, поэтому KM=CF
. Из прямоугольного треугольника AFC
находим, что
CF=\sqrt{AC^{2}-AF^{2}}=\sqrt{(a+c)^{2}-(a-c)^{2}}=2\sqrt{ac}.
Следовательно, KM=CF=2\sqrt{ac}
. Аналогично, KN=2\sqrt{bc}
и MN=2\sqrt{ab}
. Точка K
лежит между M
и N
, поэтому MN=KN+KM
, или 2\sqrt{ab}=2\sqrt{bc}+2\sqrt{ac}
. Разделив обе части этого равенства на 2\sqrt{abc}
, получим, что \frac{1}{\sqrt{c}}=\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{b}}
.
