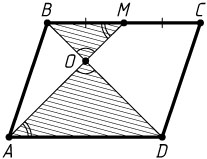
3010. Через середину M
стороны BC
параллелограмма ABCD
, площадь которого равна 1, и вершину A
проведена прямая, пересекающая диагональ BD
в точке O
. Найдите площадь четырёхугольника OMCD
.
Ответ. \frac{5}{12}
Указание. Найдите отношение \frac{BO}{OD}
.
Решение. Из подобия треугольников BOM
и DOA
находим, что
\frac{BO}{OD}=\frac{BM}{AD}=\frac{1}{2}.
Поэтому \frac{BO}{BD}=\frac{1}{3}
, а так как \frac{BM}{BC}=\frac{1}{2}
, то (см. задачу 3007)
S_{\triangle BOM}=\frac{1}{3}\cdot\frac{1}{2}S_{\triangle BCD}=\frac{1}{3}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{12}.
Следовательно,
S_{OMCD}=S_{\triangle BCD}-S_{\triangle BOM}=\frac{1}{2}-\frac{1}{12}=\frac{5}{12}.