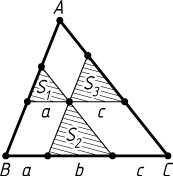
3028. Через некоторую точку, взятую внутри треугольника, проведены три прямые, параллельные сторонам. Эти прямые разбивают треугольник на шесть частей, три из которых — треугольники с площадями S_{1}
, S_{2}
, S_{3}
. Найдите площадь данного треугольника.
Ответ. (\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}})^{2}
.
Указание. Каждый из получившихся трёх треугольников подобен данному. Найдите коэффициенты подобия.
Решение. Каждый из получившихся треугольников подобен данному с коэффициентом соответственно \frac{\sqrt{S_{1}}}{\sqrt{S}}
, \frac{\sqrt{S_{2}}}{\sqrt{S}}
, \frac{\sqrt{S_{3}}}{\sqrt{S}}
, где S
— искомая площадь данного треугольника ABC
.
Обозначим стороны этих треугольников, параллельные стороне BC
треугольника ABC
, через a
, b
и c
соответственно. Тогда
a+b+c=BC,
\frac{\sqrt{S_{1}}}{\sqrt{S}}=\frac{a}{BC},~\frac{\sqrt{S_{2}}}{\sqrt{S}}=\frac{b}{BC},~\frac{\sqrt{S_{3}}}{\sqrt{S}}=\frac{c}{BC}.
Сложив почленно последние три равенства, получим:
\frac{\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}}}{\sqrt{S}}=\frac{a+b+c}{BC}=1.
Отсюда находим, что
\sqrt{S}=\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}}.
Следовательно,
S=(\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}})^{2}.