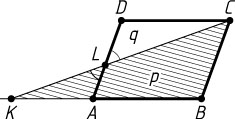
3053. Дан параллелограмм ABCD
. Прямая, проходящая через вершину C
, пересекает прямые AB
и AD
в точках K
и L
. Площади треугольников KBC
и CDL
равны p
и q
. Найдите площадь параллелограмма ABCD
.
Ответ. 2\sqrt{pq}
.
Указание. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Решение. Рассмотрим случай, когда точка L
лежит на стороне AD
. Пусть S
— площадь треугольника AKL
. Тогда коэффициент подобия треугольников AKL
и BKC
равен \frac{\sqrt{S}}{\sqrt{p}}
, а треугольников AKL
и DCL
— \frac{\sqrt{S}}{\sqrt{p}-\sqrt{S}}
. Поэтому
S=q\left(\frac{\sqrt{S}}{\sqrt{p}-\sqrt{S}}\right)^{2}.
Отсюда находим, что
q=(\sqrt{p}-\sqrt{S})^{2},~\sqrt{S}=\sqrt{p}-\sqrt{q}.
Следовательно,
S_{ABCD}=p-S+q=p-(\sqrt{p}-\sqrt{q})^{2}+q=2\sqrt{pq}.