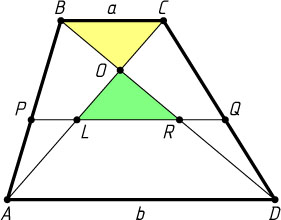
3145. Дана трапеция ABCD
. Параллельно её основаниям проведена прямая, пересекающая боковые стороны AB
и CD
соответственно в точках P
и Q
, а диагонали AC
и BD
соответственно в точках L
и R
. Диагонали AC
и BD
пересекаются в точке O
. Известно, что BC=a
, AD=b
, а площади треугольников BOC
и LOR
равны. Найдите PQ
, если точка L
лежит между точками A
и O
.
Ответ. \frac{a(3b-a)}{b+a}
.
Указание. Докажите, что \frac{AL}{AC}=\frac{b-a}{b+a}
.
Решение. Из условия задачи следует, что b\gt a
. Треугольники BOC
и ROL
подобны. Коэффициент подобия равен квадратному корню из отношения их площадей, т. е. 1. Следовательно, эти треугольники равны.
Из подобия треугольников BOC
и DOA
следует, что
\frac{AO}{OC}=\frac{AD}{BC}=\frac{b}{a}.
Поэтому
\frac{AL}{LC}=\frac{b-a}{2a},~\frac{AL}{AC}=\frac{b-a}{b+a}.
Из подобия треугольников APL
и ABC
следует, что
\frac{PL}{BC}=\frac{AL}{AC}.
Отсюда находим, что
PL=BC\cdot\frac{AL}{AC}=\frac{a(b-a}{b+a}.
Аналогично RQ=\frac{a(b-a)}{b+a}
. Следовательно,
PQ=PL+LR+RQ=\frac{2a(b-a)}{b+a}+a=\frac{a(3b-a)}{b+a}.