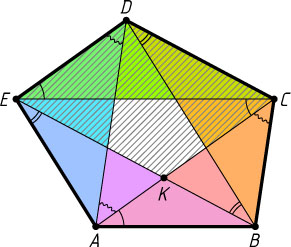
3166. Каждая диагональ выпуклого пятиугольника ABCDE
отсекает от него треугольник единичной площади. Вычислите площадь пятиугольника ABCDE
.
Ответ. \frac{5+\sqrt{5}}{2}
.
Указание. Докажите, что диагонали данного пятиугольника параллельны его сторонам.
Решение. Пусть K
— точка пересечения диагоналей AC
и BE
. Поскольку S_{\triangle ABE}=S_{\triangle ABC}
, то S_{\triangle AKE}=S_{\triangle BKC}
. Поэтому AK\cdot KE=BK\cdot KC
, или \frac{AK}{KC}=\frac{BK}{KE}
. Следовательно, EC\parallel AB
. Аналогично докажем, что остальные диагонали также параллельны соответствующим сторонам.
Поскольку DEKC
— параллелограмм, то S_{\triangle EKC}=S_{\triangle EDC}=1
. Обозначим S_{\triangle AKE}=x
. Тогда
\frac{S_{AKE}}{S_{\triangle AKB}}=\frac{EK}{KB}=\frac{x}{1-x}=\frac{S_{\triangle EKC}}{S_{\triangle CKB}}=\frac{1}{x}.
Из уравнения \frac{x}{1-x}=\frac{1}{x}
находим, что x=\frac{\sqrt{5}-1}{2}
. Следовательно,
S_{ABCDE}=S_{\triangle ABC}+S_{DEKC}+S_{\triangle AKE}=1+2+x=\frac{5+\sqrt{5}}{2}.