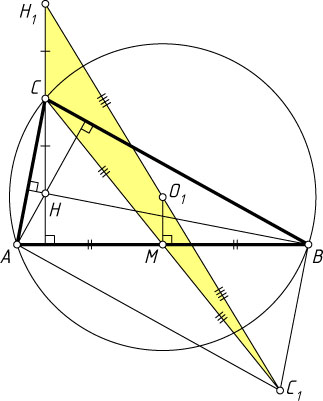
3179. В треугольнике ABC
точка H_{1}
симметрична ортоцентру H
относительно вершины C
, а точка C_{1}
симметрична точке C
относительно середины стороны AB
. Докажите, что центр O
окружности, описанной около треугольника ABC
, является серединой отрезка H_{1}C_{1}
.
Указание. Расстояние от ортоцентра треугольника до вершины вдвое больше расстояния от центра описанной окружности до противоположной стороны, т. е., если M
— середина стороны AB
, то HC=2OM
(см. задачу 1257).
Решение. Воспользуемся следующим известным фактом: расстояние от ортоцентра треугольника до вершины вдвое больше расстояния от центра описанной окружности до противоположной стороны, т. е., если M
— середина стороны AB
, то HC=2OM
(см. задачу 1257).
Пусть O_{1}
— точка пересечения серединного перпендикуляра к стороне AB
с отрезком C_{1}H_{1}
. Тогда MO_{1}\parallel CH_{1}
, а так как M
— середина CC_{1}
, то MO_{1}
— средняя линия треугольника CC_{1}H_{1}
. Значит, O_{1}
— середина отрезка C_{1}H_{1}
и
MO_{1}=\frac{1}{2}CH_{1}=\frac{1}{2}HC=OM.
Следовательно, точка O_{1}
совпадает с центром O
описанной окружности треугольника ABC
. Что и требовалось доказать