3288. На сторонах AC
и BC
треугольника ABC
вне треугольника построены квадраты ACDE
и BFKC
. Точка M
— середина стороны AB
.
а) Докажите, что CM=\frac{1}{2}DK
.
б) Найдите расстояния от точки M
до центров квадратов, если AC=6
, BC=10
и \angle ACB=30^{\circ}
.
Ответ. 7.
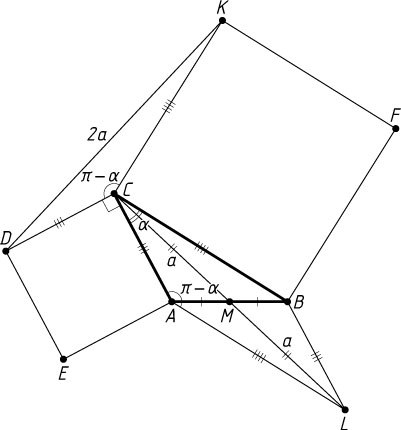
Указание. Достройте треугольник ABC
до параллелограмма ACBL
и докажите равенство треугольников DCK
и LBC
.
Решение. а) Обозначим \angle ACB=\alpha
. Отложим на продолжении медианы CM
за точку M
отрезок ML=CM
(рис. 1). Тогда четырёхугольник ACBL
— параллелограмм, поэтому
CD=AC=BL,~CK=BC,\angle CBL=180^{\circ}-\angle ACB=180^{\circ}-\alpha,
\angle DCK=360^{\circ}-90^{\circ}-90^{\circ}-\alpha=180^{\circ}-\alpha=\angle CBL,
значит, треугольники DCK
и LBC
равны по двум сторонам и углу между ними. Поэтому CL=DK
. Следовательно, CM=\frac{1}{2}CL=\frac{1}{2}DK
.
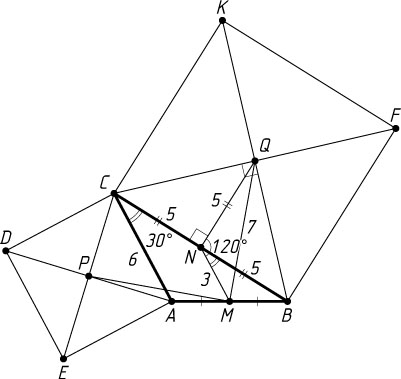
б) Пусть P
и Q
— центры квадратов ACDE
и BFKC
соответственно, N
— середина стороны BC
(рис. 2). В треугольнике MNQ
известно, что
NM=\frac{1}{2}AC=3,~NQ=\frac{1}{2}CK=5,~\angle MNQ=90^{\circ}+30^{\circ}=120^{\circ}.
По теореме косинусов
MQ=\sqrt{NM^{2}+NQ^{2}-2NM\cdot NQ\cos120^{\circ}}=\sqrt{9+25+2\cdot3\cdot5\cdot\frac{1}{2}}=7.
Аналогично находим, что MP=7
.