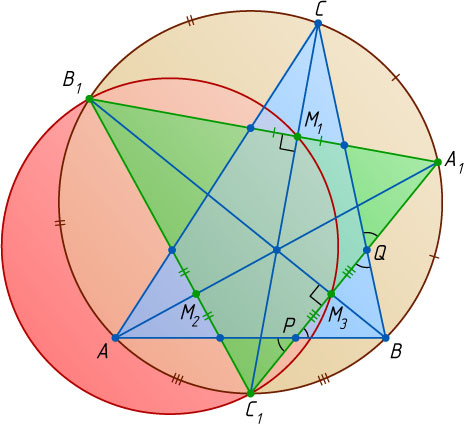
3346. Треугольник ABC
вписан в окружность. A_{1}
— середина дуги BC
, B_{1}
— середина дуги AC
, C_{1}
— середина дуги AB
. Стороны треугольника ABC
высекают на отрезках A_{1}B_{1}
, B_{1}C_{1}
, A_{1}C_{1}
меньшие отрезки с серединами M_{1}
, M_{2}
, M_{3}
. Докажите, что точки B_{1}
, C_{1}
и точки M_{1}
, M_{3}
лежат на одной окружности.
Решение. Пусть отрезок A_{1}C_{1}
пересекает стороны AB
и BC
треугольника ABC
в точках P
и Q
соответственно. Тогда
\angle BPQ=\angle BPA_{1},~\angle BQP=\angle BQC_{1}.
Угловая величина угла BPA_{1}
равна полусумме угловых величин меньших дуг BA_{1}
и AC_{1}
(см. задачу 26), а угловая величина угла BQC_{1}
— полусумме угловых величин соответственно равных им меньших дуг CA_{1}
и BC_{1}
, значит, \angle BPQ=\angle BQP
, т. е. треугольник BPQ
— равнобедренный. Его медиана BM_{3}
является высотой и биссектрисой, поэтому точки B
, M_{3}
и B_{1}
лежат на одной прямой и \angle B_{1}M_{3}C_{1}=90^{\circ}
. Аналогично, \angle B_{1}M_{1}C_{1}=90^{\circ}
, значит, из точек M_{3}
и M_{1}
отрезок B_{1}C_{1}
виден под прямым углом. Следовательно, эти точки лежат на окружности с диаметром B_{1}C_{1}
. Что и требовалось доказать.