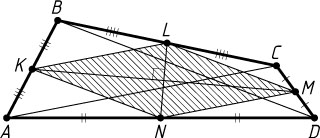
3371. Отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, взаимно перпендикулярны и равны 2 и 7. Найдите площадь четырёхугольника.
Ответ. 14.
Указание. Четырёхугольник с вершинами в серединах сторон данного четырёхугольника — параллелограмм, причём площадь этого параллелограмма вдвое меньше площади данного четырёхугольника (см. задачи 1204 и 3019).
Решение. Пусть K
, L
, M
и N
середины сторон соответственно AB
, BC
, CD
и AD
выпуклого четырёхугольника ABCD
, LN=2
, KM=7
.
Отрезки KL
и MN
— средние линии треугольников ABC
и ADC
, поэтому KL\parallel AC
, KL=\frac{1}{2}AC
, MN\parallel AC
, MN=\frac{1}{2}AC
, значит, четырёхугольник KLMN
— параллелограмм, а так как его диагонали KM
и LN
перпендикулярны, то это — ромб. Площадь ромба равна половине произведения его диагоналей, т. е. S_{KLMN}=\frac{1}{2}\cdot2\cdot7=7
.
Поскольку KL
— средняя линия треугольника ABC
, площадь треугольника KBL
равна четверти площади треугольника ABC
. Аналогично, площадь треугольника MDN
равна четверти площади треугольника ADC
, поэтому
S_{\triangle KBL}+S_{\triangle MDN}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{4}S_{\triangle ADC}=\frac{1}{4}(S_{\triangle ABC}+S_{\triangle ADC})=\frac{1}{4}S_{ABCD}.
Аналогично, S_{\triangle KAN}+S_{\triangle MCL}=\frac{1}{4}S_{ABCD}
. Следовательно,
S_{KLMN}=S_{ABCD}-S_{\triangle KBL}-S_{\triangle MDN}-S_{\triangle KAN}-S_{\triangle MCL}=
=S_{ABCD}-\frac{1}{4}S_{ABCD}-\frac{1}{4}S_{ABCD}=S_{ABCD}-\frac{1}{2}S_{ABCD}=\frac{1}{2}S_{ABCD},
S_{ABCD}=2S_{KLMN}=2\cdot7=14.