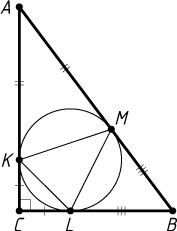
3385. Катеты прямоугольного треугольника равны 3 и 4. Найдите площадь треугольника с вершинами в точках касания вписанной окружности со сторонами треугольника.
Ответ. \frac{6}{5}
.
Решение. Пусть окружность, вписанная в прямоугольный треугольник ABC
касается катетов AC=4
и BC=3
в точках K
и L
соответственно, а гипотенузы AB
— в точке M
. Тогда
S_{\triangle ABC}=6,~AB=5,~CK=CL=\frac{1}{2}(AC+BC-AB)=\frac{1}{2}(4+3-5)=1
(см. задачу 219),
AM=AK=AC-CK=4-1=3,~BM=BL=BC-CL=3-1=2,
поэтому (см. задачу 3007)
S_{\triangle KCL}=\frac{CL}{CB}\cdot\frac{CK}{CA}\cdot S_{\triangle ABC}=\frac{1}{3}\cdot\frac{1}{4}\cdot6=\frac{1}{2},
S_{\triangle MBL}=\frac{BM}{BA}\cdot\frac{BL}{BC}\cdot S_{\triangle ABC}=\frac{2}{5}\cdot\frac{2}{3}\cdot6=\frac{8}{5},
S_{\triangle AMK}=\frac{AM}{AB}\cdot\frac{AK}{AC}\cdot S_{\triangle ABC}=\frac{3}{5}\cdot\frac{3}{4}\cdot6=\frac{27}{10}.
Следовательно,
S_{\triangle KLM}=S_{\triangle ABC}-S_{\triangle KCL}-S_{\triangle MBL}-S_{\triangle AMK}=6-\frac{1}{2}-\frac{8}{5}-\frac{27}{10}=\frac{6}{5}.