3447. На сторонах AB
, BC
, CD
и AD
параллелограмма ABCD
отмечены точки K
, L
, M
и N
соответственно, причём \frac{AK}{KB}=\frac{BL}{LC}=\frac{CM}{MD}=\frac{DN}{NA}
.
а) Докажите, что четырёхугольник KLMN
— параллелограмм, а его центр совпадает с центром параллелограмма ABCD
.
б) Найдите отношение площадей параллелограммов KLMN
и ABCD
, если известно, что \frac{AK}{KB}=2
.
Ответ. 5:9
.
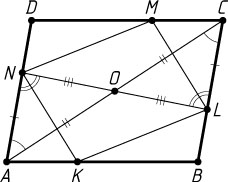
Решение. а) Пусть диагональ NL
четырёхугольника KLMN
и диагональ AC
параллелограмма ABCD
пересекаются в точке O
(рис. 1). Треугольники AON
и COL
равны по стороне (AN=CL
, так как эти отрезки составляют одну и ту же часть от равных отрезков AD
и BC
) и двум прилежащим к ней углам. Значит, OL=ON
и AO=OC
. Поэтому O
— центр параллелограмма ABCD
. Аналогично докажем, что диагональ KM
четырёхугольника KLMN
проходит через точку O
и делится ею пополам. Следовательно, KLMN
— параллелограмм с центром O
.
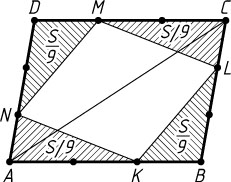
б) Обозначим S_{ABCD}=S
(рис. 2). Тогда
S_{\triangle ABC}=\frac{1}{2}S,~S_{\triangle BKL}=\frac{BK}{BA}\cdot\frac{BL}{BC}S_{\triangle ABC}=\frac{1}{3}\cdot\frac{2}{3}\cdot\frac{1}{2}S=\frac{1}{9}S
(см. задачу 3007). Аналогично
S_{\triangle MDN}=\frac{1}{9}S,~S_{\triangle MCL}=\frac{1}{9}S,~S_{\triangle KAN}=\frac{1}{9}S.
Значит,
S_{KLMN}=S-4\cdot\frac{1}{9}S=\frac{5}{9}S.
Следовательно, \frac{S_{KLMN}}{S_{ABCD}}=\frac{5}{9}
.