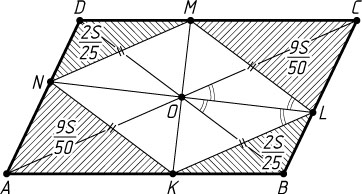
3448. Вершины ромба расположены (по одной) на сторонах параллелограмма.
а) Докажите, что центры ромба и параллелограмма совпадают.
б) Найдите отношение площадей ромба и параллелограмма, если известно, что стороны ромба параллельны диагоналям параллелограмма, а диагонали параллелограмма относятся как 2:3
.
Ответ. 12:25
.
Решение. а) Известно, что если вершины одного параллелограмма лежат на сторонах другого параллелограмма (по одной), то центры параллелограммов совпадают (см. 1057).
б) Пусть ABCD
— данный параллелограмм, в котором \frac{BD}{AC}=\frac{2}{3}
, а вершины K
, L
, M
, N
ромба KLMN
лежат на отрезках AB
, BC
, CD
, AD
соответственно. Центр O
параллелограмма является также центром ромба, а так как стороны ромба параллельны диагоналям параллелограмма и LO
— биссектриса треугольника KLM
, то OL
— биссектриса треугольника BOC
. По свойству биссектрисы треугольника
\frac{BL}{LC}=\frac{OB}{OC}=\frac{\frac{1}{2}BD}{\frac{1}{2}AC}=\frac{2}{3}.
Значит, \frac{BK}{AB}=\frac{BL}{BC}=\frac{2}{5}
и \frac{CM}{CD}=\frac{CL}{BC}=\frac{3}{5}
.
Пусть площадь параллелограмма равна S
. Треугольник BKL
подобен треугольнику BAC
с коэффициентом \frac{2}{5}
, поэтому
S_{\triangle DMN}=S_{\triangle KBL}=\left(\frac{2}{5}\right)^{2}S_{\triangle BAC}=\frac{4}{25}\cdot\frac{1}{2}S=\frac{2}{25}S.
Аналогично
S_{\triangle AKN}=S_{\triangle CML}=\left(\frac{3}{5}\right)^{2}S_{\triangle CDB}=\frac{9}{25}\cdot\frac{1}{2}S=\frac{9}{50}S.
Значит,
S_{KLMN}=S-2\cdot\frac{2}{25}S-2\cdot\frac{9}{50}S=\frac{12}{25}S.
Следовательно, \frac{S_{KLMN}}{S_{ABCD}}=\frac{12}{25}
.