3449. Окружность с центром O
вписана в равнобедренную трапецию ABCD
с основаниями AD\gt BC
.
а) Докажите, что прямая BO
делит площадь трапеции пополам.
б) Пусть M
и N
— точки касания окружности со боковыми сторонами трапеции. В каком отношении прямая MN
делит площадь трапеции, если AD=2BC
?
Ответ. 7:20
.
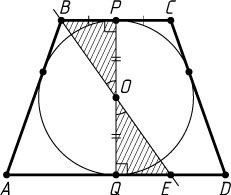
Решение. а) Пусть окружность касается оснований BC
и AD
в точках P
и Q
соответственно (рис. 1). Тогда точка O
— середина отрезка PQ
. Поскольку трапеция равнобедренная, точки P
и Q
— середины оснований.
Пусть прямая BO
пересекает основание AD
в точке E
. Прямоугольные треугольники OPB
и OQE
равны по катету и прилежащему острому углу, поэтому S_{\triangle OPB}=S_{\triangle OQE}
. Прямоугольные трапеции ABPQ
и PCDQ
равновелики, так как у них соответственно равные основания и одна и та же высота PQ
. Следовательно,
S_{\triangle ABE}=S_{ABPQ}-S_{\triangle OPB}+S_{\triangle OQE}=S_{ABPQ}=S_{PCDQ}=\frac{1}{2}S_{ABCD}.
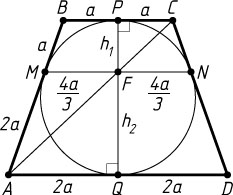
б) Пусть точки M
и N
лежат на боковых сторонах AB
и CD
соответственно (рис. 2). Положим BP=a
, AQ=2a
. Тогда
BC=2a,~AD=4a,~CN=CP=BP=BM=a,~AM=AQ=DQ=DN=2a,
значит, \frac{BM}{AM}=\frac{CN}{DN}
. Поэтому прямая MN
параллельна основаниям трапеции.
Пусть диагональ AC
пересекает отрезок MN
в точке F
. Треугольник AMF
подобен треугольнику ABC
с коэффициентом \frac{AM}{AB}=\frac{2a}{3a}=\frac{2}{3}
. Поэтому MF=\frac{2}{3}BC=\frac{4}{3}a
. Аналогично, рассматривая подобные треугольники CFN
и CAD
, получим, что NF=\frac{4}{3}a
. Значит, MN=MF+NF=\frac{8a}{3}
.
Пусть h_{1}
и h_{2}
— высоты трапеций MBCN
и AMND
соответственно. Тогда \frac{h_{1}}{h_{2}}=\frac{BM}{AM}=\frac{a}{2a}=\frac{1}{2}
. Следовательно,
\frac{S_{MBCN}}{S_{AMND}}=\frac{\frac{1}{2}(MN+BC)h_{1}}{\frac{1}{2}(MN+AD)h_{2}}=\frac{\frac{1}{2}\left(\frac{8}{3}a+2a\right)h_{1}}{\frac{1}{2}\left(\frac{8}{3}a+4a\right)h_{2}}=\frac{\frac{14}{3}ah_{1}}{\frac{20}{3}ah_{2}}=\frac{7}{10}\cdot\frac{1}{2}=\frac{7}{20}.