3451. Вершины A
и D
четырёхугольника ABCD
соединены с серединой M
стороны BC
, а вершины B
и C
— с серединой N
стороны AD
.
а) Докажите, что если середины отрезков AM
, DM
, BN
, CN
не лежат на одной прямой, то четырёхугольник с вершинами в этих серединах — параллелограмм.
б) Найдите площадь этого параллелограмма, если известно, что AD=6
, BC=8
, а угол между прямыми BC
и AD
равен 30^{\circ}
.
Ответ. 3.
Решение. а) Пусть E
, F
, G
, H
— середины отрезков AM
, DM
, BN
, CN
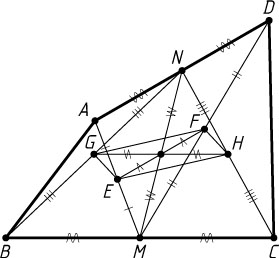
соответственно (рис. 1). Отрезок MN
— общая медиана треугольников AMD
и BNC
. Отрезок EF
— средняя линия треугольника AMD
, поэтому EF
проходит через середину медианы MN
и делится ею пополам (см. задачу 1881). Аналогично отрезок HG
также проходит через середину MN
и делится ею пополам. Значит, диагонали EF
и GH
четырёхугольника EGFH
проходят через середину MN
и делятся этой серединой пополам. Следовательно, EGFH
— параллелограмм.
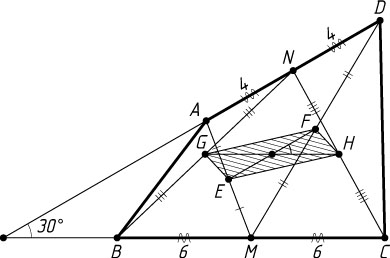
б) Диагонали параллелограмма EGFH
параллельны сторонам AD
и BC
четырёхугольника ABCD
и равны их половинам (рис. 2). Угол между этими диагоналями также равен 30^{\circ}
. Следовательно,
S_{EGFH}=\frac{1}{2}EF\cdot GH\sin30^{\circ}=\frac{1}{2}\cdot3\cdot\cdot4\frac{1}{2}=3.