3452. На стороне AB
выпуклого четырёхугольника ABCD
отмечены точки E
и F
, на стороне BC
— точки K
и L
, на стороне CD
— точки M
и N
, на стороне AD
— точки P
и Q
. При этом AE=EF=FB
, BK=KL=LC
, CM=MN=ND
и DP=PQ=QA
.
а) Докажите, что отрезки KQ
и LP
делят отрезок FM
на три равных отрезка.
б) Известно, что площадь четырёхугольника ABCD
равна 18. Найдите площадь четырёхугольника, вершины которого — точки пересечения прямых EN
, FM
, KQ
и LP
.
Ответ. 2.
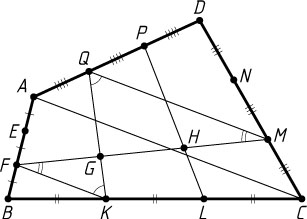
Решение. а) Пусть отрезки FM
и KQ
пересекаются в точке G
, а отрезки FM
и LP
— в точке H
(рис. 1). Поскольку \frac{BK}{BC}=\frac{BF}{BA}=\frac{1}{3}
, треугольник BKF
подобен треугольнику BCA
с коэффициентом \frac{1}{3}
. Поэтому KF\parallel AC
и KF=\frac{1}{3}AC
. Аналогично MQ\parallel AC
и MQ=\frac{2}{3}AC
. Значит, треугольник KGF
подобен треугольнику QGM
, причём коэффициент подобия равен \frac{KF}{MQ}=\frac{1}{2}
. Поэтому FG=\frac{1}{3}FM
. Аналогично докажем, что HM=\frac{1}{3}FM
. Тогда
GH=FM-FG-MH=FM-\frac{1}{3}FM-\frac{1}{3}FM=\frac{1}{3}FM.
Следовательно, FG=GH=HM
.
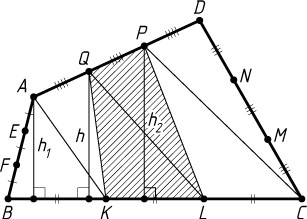
б) Сначала докажем, что площадь четырёхугольника KLPQ
в три раза меньше площади четырёхугольника ABCD
(рис. 2).
Проведём диагонали AK
, QL
и CP
четырёхугольников ABKQ
, QKLP
и PLCD
. Пусть h_{1}
, h
и h_{2}
— расстояния от точек соответственно A
, Q
и P
до прямой BC
. Тогда
h=\frac{h_{1}+h_{2}}{2},~S_{\triangle ABK}=\frac{1}{2}BK\cdot h_{1},~S_{\triangle QKL}=\frac{1}{2}KL\cdot h,~S_{\triangle PLC}=\frac{1}{2}LC\cdot h_{2}.
Следовательно, S_{\triangle KQL}=\frac{S_{\triangle ABK}+S_{\triangle PLC}}{2}
. Аналогично S_{\triangle LPQ}=\frac{S_{\triangle AQK}+S_{\triangle PCD}}{2}
. Поэтому
S_{KLPQ}=\frac{S_{\triangle KQL}+S_{\triangle LPQ}}{2}=\frac{S_{\triangle ABK}+S_{\triangle PLC}}{2}+\frac{S_{\triangle AQK}+S_{\triangle PCD}}{2}=
=\frac{S_{\triangle ABK}+S_{\triangle AQK}+S_{\triangle PLC}+S_{\triangle PCD}}{2}==\frac{S_{ABKQ}+S_{PLCD}}{2}.
Следовательно, S_{KLPQ}=\frac{1}{3}S_{ABCD}
. Что и требовалось доказать.
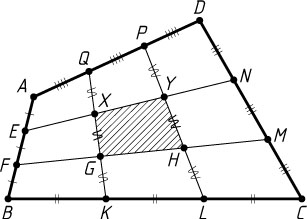
Пусть отрезки KQ
и LP
пересекают отрезок EN
в точках X
и Y
соответственно (рис. 3). Поскольку точки G
и X
делят отрезок KQ
на три равные части, а точки H
и Y
делят отрезок LP
на три равные части, то из предыдущего утверждения вытекает, что S_{GXYH}=\frac{1}{3}S_{KLPQ}
. Следовательно,
S_{GXYH}=\frac{1}{3}\cdot\frac{1}{3}S_{ABCD}=\frac{1}{9}S_{ABCD}=\frac{1}{9}\cdot18=2.