3460. В равнобедренной трапеции ABCD
с основаниями AD
и BC
расположены две окружности, каждая из которых касается другой окружности, двух боковых сторон и одного из оснований. Пусть P
и Q
— точки касания окружностей с боковой стороной AB
, а общая касательная окружностей, проходящая через их точку касания, пересекает боковые стороны в точках M
и N
.
а) Докажите, что MN=PQ
.
б) Найдите площадь трапеции ABCD
, если известно, что AD=18
и BC=2
.
Ответ. 80\sqrt{3}
.
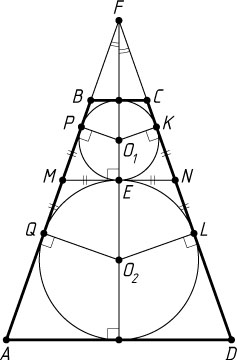
Решение. а) Пусть окружности касаются в точке E
(рис. 1), меньшая окружность с центром O_{1}
касается боковых сторон AB
и CD
в точках P
и K
соответственно, большая окружность с центром O_{2}
— в точках Q
и L
соответственно, а прямые AB
и CD
пересекаются в точке F
.
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому точки O_{1}
и O_{2}
лежат биссектрисе угла AFD
, т. е. на высоте равнобедренного треугольника ADF
.
Прямая MN
— общая касательная к окружностям, поэтому она перпендикулярна O_{1}O_{2}
, а значит, параллельна основаниям трапеции. По теореме о равенстве отрезков касательных, проведённых к окружности из одной точки, MP=ME=MQ
и NL=NE=NK
. Значит, ME=\frac{1}{2}PQ
. Аналогично NE=\frac{1}{2}KL
, а так как PQ=FQ-FP=FL-FK=KL
, то PQ=KL
. Следовательно, PQ=MN
.
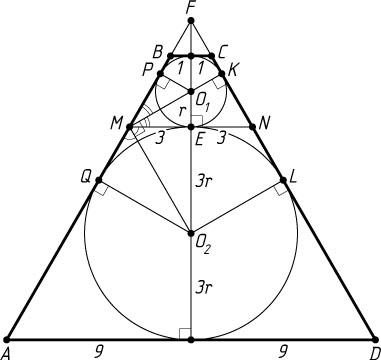
б) Треугольник FMN
подобен треугольнику FAD
(рис. 2). При этом подобии отрезок BC
в треугольнике FMN
соответствует отрезку MN
в треугольнике FAD
. Значит, коэффициент подобия, с одной стороны, равен \frac{BC}{MN}
, с другой — \frac{MN}{AD}
. Из равенства \frac{BC}{MN}=\frac{MN}{AD}
находим, что MN^{2}=BC\cdot AD=2\cdot18=36
. Значит, MN=6
, ME=\frac{1}{2}MN=3
, а коэффициент подобия равен \frac{BC}{MN}=\frac{2}{6}=\frac{1}{3}
. Тогда радиус второй окружности в три раза больше радиуса первой.
Лучи MO_{1}
и MO_{2}
— биссектрисы смежных углов BMN
и AMN
. Поэтому треугольник O_{1}MO_{2}
прямоугольный, а так как ME
— его высота, проведённая из вершины прямого угла, то ME^{2}=O_{1}E\cdot O_{2}E
, или 9=r\cdot3r
, где r
и 3r
— радиусы окружностей. Отсюда находим, что r=\sqrt{3}
. Тогда высота трапеции равна 2r+6r=8r=8\sqrt{3}
. Следовательно,
S_{ABCD}=\frac{AD+BC}{2}\cdot8r=\frac{18+2}{2}\cdot8\sqrt{3}=80\sqrt{3}.