3463. Две окружности пересекаются в точках P
и Q
. Прямая, проходящая через точку P
, второй раз пересекает первую окружность в точке A
, а вторую — в точке D
. Прямая, проходящая через точку Q
параллельно AD
, второй раз пересекает первую окружность в точке B
, а вторую — в точке C
.
а) Докажите, что четырёхугольник ABCD
— параллелограмм.
б) Найдите отношение BP:PC
, если радиус первой окружности вдвое больше радиуса второй.
Ответ. 2.
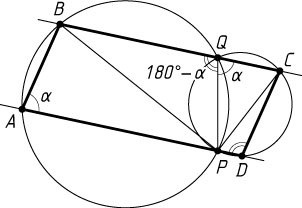
Решение. а) Обозначим \angle BAP=\alpha
(рис. 1). Четырёхугольники ABQP
и CDPQ
вписанные, поэтому
\angle BQP=180^{\circ}-\alpha,~\angle PQC=180^{\circ}-\angle BQP=180^{\circ}-(180^{\circ}-\alpha)=\alpha,~
\angle ADC=\angle PDC=180^{\circ}-\angle PQC=180^{\circ}-\alpha.
Значит, AB\parallel CD
. Противоположные стороны четырёхугольника ABCD
попарно параллельны, следовательно, это параллелограмм.
б) Пусть R
и r
— радиусы первой и второй окружностей соответственно, причём R=2r
(рис. 2). По теореме синусов
BP=2R\sin\angle BAP=4r\sin\alpha,~CP=2r\sin\angle PQC=2r\sin\alpha.
Следовательно, \frac{BP}{PC}=\frac{4r\sin\alpha}{2r\sin\alpha}=2
.