3491. Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.
Ответ. 3.
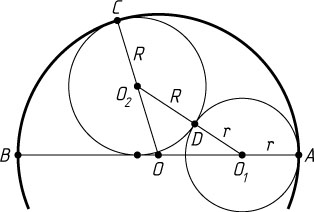
Решение. а) Пусть AB
— диаметр большей из трёх окружностей (рис. 1), O
— её центр, O_{1}
— центр окружности радиуса r
, касающейся окружности с диаметром AB
в точке A
, O_{2}
— центр окружности радиуса R
, касающейся окружности с диаметром AB
в точке C
, окружности с центром O_{1}
— в точке D
, отрезка AB
— в точке E
.
Точки O
, O_{2}
и C
лежат на одной прямой, поэтому OO_{2}=OC-O_{2}C=OC-R
. Аналогично OO_{1}=OA-O_{1}A=OA-r
и O_{1}O_{2}=O_{1}D+O_{2}D=r+R
. Следовательно, периметр треугольника OO_{1}O_{2}
равен
OO_{1}+OO_{2}+O_{1}O_{2}=OA-r+OC-R+r+R=OA+OC=2OA=AB.
б) Пусть OA=6
, r=2
. Тогда
O_{2}E=R,~O_{1}O_{2}=2+R,~OO_{1}=OA-O_{1}A=6-2=4,~OO_{2}=OC-O_{2}C=6-R.
Из прямоугольных треугольников O_{1}O_{2}E
и OO_{2}E
находим, что
O_{1}E=\sqrt{O_{1}O_{2}^{2}-O_{2}E^{2}}=\sqrt{(2+R)^{2}-R^{2}}=\sqrt{4+4R},~
OE=\sqrt{OO_{2}^{2}-O_{2}E^{2}}=\sqrt{(6-R)^{2}-R^{2}}=\sqrt{36-12R}.
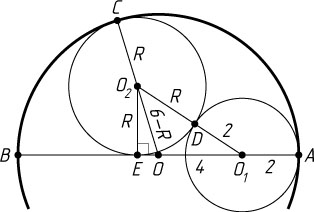
Если точка E
лежит на отрезке OB
(рис. 2), то O_{1}E=OO_{1}+OE
, или \sqrt{4+4R}=4+\sqrt{36-12R}
. Из этого уравнения находим, что R=3
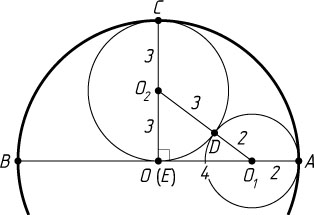
(это значит, что диаметр искомой окружности равен радиусу наибольшей из трёх окружностей, т. е. точка E
совпадает с O
).
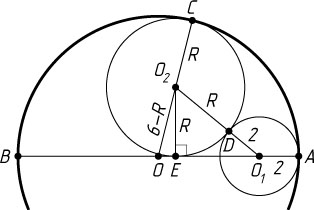
Если точка E
лежит на отрезке OA
, то аналогично получим тот же результат.