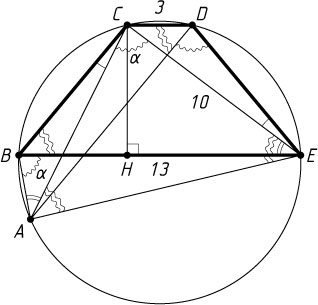
3676. В трапеции BCDE
основание BE=13
, основание CD=3
, CE=10
. На описанной около трапеции BCDE
окружности взята отличная от E
точка A
так, что CA=10
. Найдите длину отрезка BA
и площадь пятиугольника ABCDE
.
Ответ. 3; \frac{4098}{61}
.
Указание. Докажите, что \angle ACB=\angle CDE
.
Решение. Поскольку трапеция BCDE
вписана в окружность, то она равнобедренная.
Заметим, что угол CDE
— тупой, поэтому для любой точки X
, отличной от E
и лежащей на дуге CE
, содержащей точку D
, CX\lt CE=10
(в треугольнике CDE
против тупого угла лежит наибольшая сторона). Следовательно, точка не может лежать на этой дуге. Точка A
не может лежать и на дуге BC
, не содержащей точки D
(CB=DE\lt CE=10
). Таким образом, точка A
лежит на дуге BE
, не содержащей точки C
.
Докажем равенство углов \angle ACB
и \angle CED
. Действительно, \angle BAC=\angle BEC=\angle DCE
, а так как
\angle ABE=\angle ACE=\angle ADE~\mbox{и}~\angle CBE=\angle CAE=\angle CEA=\angle ADC,
то
\angle ABC=\angle ABE+\angle CBE=\angle ADE+\angle ADC=\angle CDE.
Поэтому равны и углы \angle ACB=\angle CED
(как оставшиеся углы треугольников ABC
и CDE
). Следовательно, равны и хорды, на которые опираются эти углы, т. е. AB=CD=3
.
Обозначим \angle ABE=\angle ACE=\alpha
. Из треугольников ABE
и ACE
по теореме косинусов находим, что
AE^{2}=AB^{2}+BE^{2}-2AB\cdot BE\cdot\cos\alpha=9+169-2\cdot3\cdot13\cdot\cos\alpha=178-78\cos\alpha,
AE^{2}=AC^{2}+CE^{2}-2AC\cdot CE\cdot\cos\alpha=100+100-2\cdot10\cdot10\cdot\cos\alpha=200-200\cos\alpha.
Из уравнения 178-78\cos\alpha=200-200\cos\alpha
находим \cos\alpha=\frac{11}{61}
. Тогда
\sin\alpha=\sqrt{1-\cos^{2}\alpha}=\sqrt{1-\frac{11^{2}}{61^{2}}}=\frac{\sqrt{(61-11)(61+11)}}{61}=\frac{60}{61}.
Поэтому
S_{\triangle ABE}=\frac{1}{2}AB\cdot BE\cdot\sin\alpha=\frac{1}{2}\cdot3\cdot13\cdot\frac{60}{61}=\frac{3\cdot13\cdot30}{61}.
Пусть CH
— высота равнобедренной трапеции BCDE
. Тогда
EH=\frac{BE+CD}{2}=\frac{13+3}{2}=8.
Из прямоугольного треугольника CHE
находим, что
CH=\sqrt{CE^{2}-EH^{2}}=\sqrt{100-64}=6.
Поэтому S{BCDE}=\frac{BE+CD}{2}\cdot CH=8\cdot6=48
.
Следовательно,
S_{BCDEA}=S_{BCDE}+S_{\triangle ABE}=48+\frac{3\cdot13\cdot30}{61}=\frac{4098}{61}.