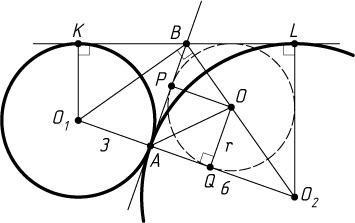
3761. Окружности радиусов 3 и 6 с центрами соответственно в точках и O_{1}
и O_{2}
касаются внешним образом в точке A
. К окружностям проведены общая внешняя касательная и общая внутренняя касательная. Эти касательные пересекаются в точке B
, а L
— общая точка внешней касательной и окружности радиуса 6. Найдите радиус окружности, вписанной в четырёхугольник ABLO_{2}
.
Ответ. 6(\sqrt{2}-1)
.
Указание. Докажите, что BA
— высота прямоугольного треугольника O_{1}BO_{2}
, проведённая из вершины прямого угла B
.
Решение. Пусть K
— точка касания общей внешней касательной с окружностью радиуса 3. Поскольку BO_{1}
и BO_{2}
— биссектрисы углов ABK
и ABL
, то \angle O_{1}BO_{2}
, значит, BA
— высота прямоугольного треугольника O_{1}BO_{2}
, проведённая из вершины прямого угла, поэтому
BA=\sqrt{AO_{1}\cdot AO_{2}}=3\sqrt{2}.
Тогда BL=BA=3\sqrt{2}
как отрезки касательных, проведённых к окружности из одной точки. Поскольку BL+AO_{2}=BA+LO_{2}
, то в четырёхугольник ABLO_{2}
можно вписать окружность. Центр O
этой окружности лежит диагонали BO_{2}
, так как BO_{2}
— биссектриса углов при вершинах B
и O_{2}
этого четырёхугольника.
Пусть P
и Q
— точки касания искомой окружности с отрезками BA
и AO_{2}
соответственно, а r
— искомый радиус. Тогда
S_{\triangle ABO_{2}}=S_{\triangle AOO_{2}}+S_{\triangle AOB}=\frac{1}{2}\cdot AO_{2}\cdot OQ+\frac{1}{2}\cdot AB\cdot OP=
\frac{1}{2}\cdot6\cdot r+\frac{1}{2}\cdot3\sqrt{2}\cdot r=\frac{1}{2}\cdot r(6+3\sqrt{2}).
С другой стороны,
S_{\triangle ABO_{2}}=\frac{1}{2}\cdot AO_{2}\cdot AB=\frac{1}{2}\cdot6\cdot3\sqrt{2}=\frac{1}{2}\cdot18\sqrt{2}.
Из уравнения \frac{1}{2}\cdot r(6+3\sqrt{2})=\frac{1}{2}\cdot18\sqrt{2}
находим, что
r=\frac{6}{1+\sqrt{2}}=6(\sqrt{2}-1).