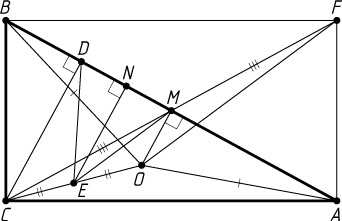
3791. Внутри прямоугольного треугольника ABC
(угол C
— прямой) взята точка O
так, что OA=OB=b
. В треугольнике ABC
CD
— высота, точка E
— середина отрезка OC
, DE=a
. Найдите CE
.
Ответ. \frac{1}{2}\sqrt{2b^{2}-4a^{2}}
.
Указание. Достройте данный треугольник до прямоугольника и воспользуйтесь утверждением: «Суммы квадратов расстояний от произвольной точки до противоположных вершин прямоугольника равны» (см. задачу 2169).
Решение. Пусть M
и N
— проекции точек соответственно O
и E
на гипотенузу AB
. Заметим, что M
середина AB
.
Поскольку EN\parallel OM\parallel CD
и E
— середина OC
, то EN
— средняя линия трапеции COMD
, поэтому N
— середина отрезка MD
. Высота EN
треугольника DEM
является его медианой, поэтому треугольник DEM
— равнобедренный. Следовательно, EM=ED=a
.
На продолжении отрезка CM
за точку M
отложим отрезок MF
, равный CM
. Тогда ACBF
— прямоугольник, EM
— средняя линия треугольника COF
, OF=2\cdot EM=2a
.
Таким образом, нам известны расстояния от точки O
до трёх вершин прямоугольника ACBF
. Поскольку OC^{2}+OF^{2}=OA^{2}+OB^{2}
(см. задачу 2169), то
OC^{2}=OA^{2}+OB^{2}-OF^{2}=b^{2}+b^{2}-4a^{2}=2b^{2}-4a^{2}.
Следовательно, CE=\frac{1}{2}OC=\frac{1}{2}\sqrt{2b^{2}-4a^{2}}
.