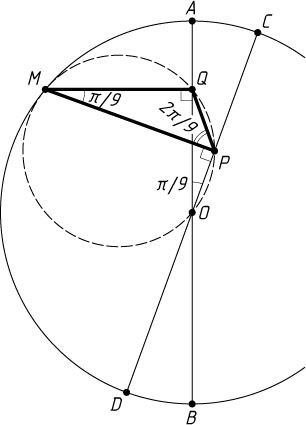
3835. В окружности радиуса 4 с центром в точке O
проведены два диаметра AB
и CD
так, что \angle AOC=\frac{\pi}{9}
. Из точки M
, лежащей на окружности и отличной от точек A
, B
, C
и D
, проведены к диаметрам AB
и CD
перпендикуляры MQ
и MP
соответственно (точка Q
лежит на AB
, а точка P
на CD
) так, что \angle MPQ=\frac{2\pi}{9}
. Найдите площадь треугольника MPQ
.
Ответ. S=4\sqrt{3}\sin{\frac{\pi}{9}}\sin{\frac{2\pi}{9}}
.
Указание. Докажите, что точки P
и Q
лежат на окружности с диаметром OM
. Если r
— радиус этой окружности, то
S_{\triangle MPQ}=2r^{2}\sin\angle QMP\sin\angle MPQ\sin\angle MQP.
Решение. Докажем сначала, что площадь S
треугольника можно вычислить по формуле:
S=2R^{2}\sin\alpha\sin\beta\sin\gamma,
где \alpha
, \beta
, \gamma
— углы треугольника, а R
— радиус его описанной окружности.
Действительно, если b
и c
— стороны треугольника, противолежащие углам соответственно \beta
и \gamma
, то
S=\frac{1}{2}\cdot bc\cdot\sin\alpha=\frac{1}{2}\cdot2R\sin\beta\cdot2R\sin\gamma\cdot\sin\alpha=2R^{2}\sin\alpha\sin\beta\sin\gamma,
что и требовалось доказать.
Из условия данной задачи следует, что из точек P
и Q
отрезок OM
виден под прямым углом. Это значит, что точки P
и Q
лежат на окружности с диаметром OM
. Если r
— радиус этой окружности, то r=\frac{1}{2}OM=2
.
По теореме о вписанных углах, опирающихся на одну дугу
\angle QMP=\angle QOP=\angle AOC=\frac{\pi}{9},
поэтому
\angle MQP=\pi-\angle QMP-\angle MPQ=\pi-\frac{\pi}{9}-\frac{2\pi}{9}=\pi-\frac{\pi}{3}.
По ранее доказанному
S_{\triangle MPQ}=2r^{2}\sin\angle QMP\sin\angle MPQ\sin\angle MQP=8\sin\frac{\pi}{9}\sin\frac{2\pi}{9}\sin\frac{\pi}{3}=
=4\sqrt{3}\sin{\frac{\pi}{9}}\sin{\frac{2\pi}{9}}.