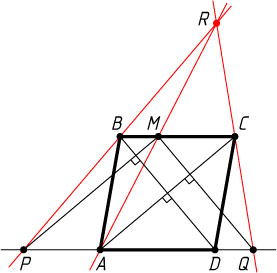
3956. На стороне BC
ромба ABCD
выбрана точка M
. Прямые, проведённые через M
перпендикулярно диагоналям BD
и AC
, пересекают прямую AD
в точках P
и Q
соответственно. Оказалось, что прямые PB
, QC
и AM
пересекаются в одной точке. Чему может быть равно отношение \frac{BM}{MC}
?
Ответ. \frac{1}{2}
.
Указание. Пусть прямые PB
, QC
и AM
пересекаются в точке R
. Тогда BC
— средняя линия треугольника PRQ
.
Решение. Прямые MP
и AC
параллельны, так как они перпендикулярны одной и той же прямой BD
(диагонали ромба перпендикулярны). Аналогично MQ\parallel BD
. Значит, четырёхугольники ACMP
и BMQD
— параллелограммы. Поэтому AP=MC
и DQ=BM
. Тогда
PQ=AP+AD+DQ=BM+BC+CM=BC+AD=2BC.
Пусть прямые PB
, QC
и AM
пересекаются в точке R
. Поскольку BC\parallel PQ
и BC=\frac{1}{2}PQ
, отрезок BC
— средняя линия треугольника PRQ
. Значит, BM
— средняя линия треугольника ARP
. Тогда
BM=\frac{1}{2}AP=\frac{1}{2}MC.
Следовательно, \frac{BM}{MC}=\frac{1}{2}
.