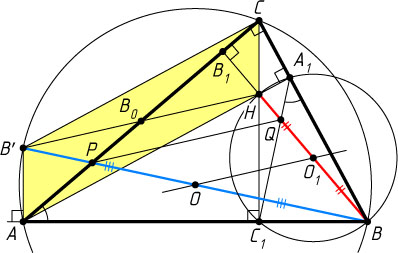
3959. В неравнобедренном остроугольном треугольнике ABC
проведены высоты AA_{1}
и CC_{1}
, H
— точка пересечения высот, O
— центр описанной окружности, B_{0}
— середина стороны AC
. Прямая BO
пересекает сторону AC
в точке P
, а прямые BH
и A_{1}C_{1}
пересекаются в точке Q
. Докажите, что прямые HB_{0}
и PQ
параллельны.
Указание. Треугольник A_{1}BC_{1}
подобен треугольнику ABC
. Пусть O_{1}
— центр описанной окружности треугольника A_{1}BC_{1}
, а BB'
диаметр описанной окружности треугольника ABC
. Тогда OO_{1}\parallel PQ
, а отрезок HB'
проходит через точку B_{0}
.
Решение. Из точек A_{1}
и C_{1}
отрезок BH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BH
и центром в середине O_{1}
отрезка BH
. Поскольку \angle BA_{1}C_{1}=\angle BAC
, треугольник A_{1}BC_{1}
подобен треугольнику ABC
по двум углам. При этом подобии диаметр BH
описанной окружности треугольника A_{1}BC_{1}
соответствует диаметру BB'
описанной окружности треугольника ABC
, а точка Q
пересечения диаметра первой окружности со стороной A_{1}C_{1}
треугольника A_{1}BC_{1}
— точке P
пересечения диаметра второй окружности со стороной AC
треугольника ABC
. Значит, \frac{BQ}{BH}=\frac{BP}{BB'}
. Следовательно, QP\parallel OO_{1}
.
Точка A
лежит на окружности с диаметром BB'
, поэтому AB'\perp AB
, а так как CC_{1}\perp AB
, то AB'\parallel CC_{1}
. Аналогично CB'\parallel AA_{1}
. Противоположные стороны четырёхугольника AHCB'
попарно параллельны, значит, это параллелограмм. Его диагональ HB'
проходит через середину B_{0}
диагонали AC
.
Отрезок OO_{1}
— средняя линия треугольника BHB'
, значит, OO_{1}\parallel HB'
, а так как OO_{1}\parallel PQ
, то PQ\parallel HB'
. Следовательно, PQ\parallel HB_{0}
. Что и требовалось доказать.