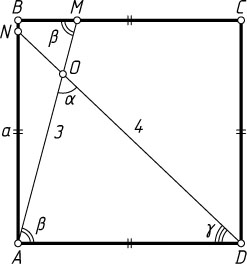
4133. В квадрате ABCD
точка M
лежит на стороне BC
, а точка N
— на стороне AB
. Прямые AM
и DN
пересекаются в точке O
. Найдите площадь квадрата, если известно, что DN=4
, AM=3
, а косинус угла DOA
равен q
.
Ответ. \frac{144q^{2}}{25-24\sqrt{1-q^{2}}}
.
Указание. Обозначьте
\angle AOD=\alpha,~\angle AMB=\angle DAM=\beta,~\angle ADN=\gamma
и составьте тригонометрическое уравнение относительно \gamma
.
Решение. Пусть сторона квадрата равна a
. Обозначим,
\angle AOD=\alpha,~\angle AMB=\angle DAM=\beta,~\angle ADN=\gamma.
Из прямоугольных треугольников ABM
и DAN
находим, что
\sin\beta=\frac{AB}{AM}=\frac{a}{3},~\cos\gamma=\frac{AD}{DN}=\frac{a}{4}.
Отсюда следует, что
4\cos\gamma=3\sin\beta=3\sin(180^{\circ}-\alpha-\gamma)=3\sin(\alpha+\gamma)=3\sin\alpha\cos\gamma+3\cos\alpha\sin\gamma.
Разделив на \cos\gamma
обе части уравнения
4\cos\gamma=3\sin\alpha\cos\gamma+3\cos\alpha\sin\gamma,
получим, что
3\sin\alpha+3\cos\alpha\tg\gamma=4,
откуда
\tg\gamma=\frac{4-3\sin\alpha}{3\cos\alpha}=\frac{4-3\sqrt{1-q^{2}}}{3q}.
Тогда
\cos^{2}\gamma=\frac{1}{1+\tg^{2}\gamma}=\frac{9q^{2}}{9q^{2}+16-24\sqrt{1-q^{2}}+9(1-q^{2})}=\frac{9q^{2}}{25-24\sqrt{1-q^{2}}}.
Следовательно,
S_{ABCD}=a^{2}=(4\cos\gamma)^{2}=\frac{144q^{2}}{25-24\sqrt{1-q^{2}}}.