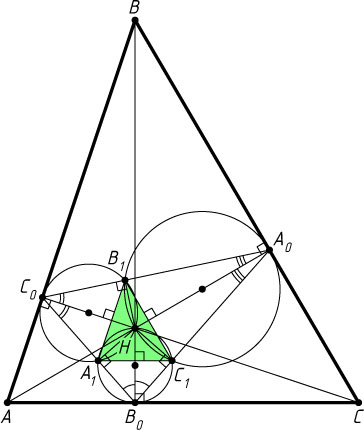
4162. Через точку пересечения высот остроугольного треугольника ABC
проходят три окружности, каждая из которых касается одной из сторон треугольника в основании высоты. Докажите, что вторые точки пересечения окружностей являются вершинами треугольника, подобного исходному.
Указание. Докажите что вторые точки пересечения окружностей лежат на сторонах треугольника с вершинами в основаниях высот треугольника ABC
.
Решение. Пусть высоты AA_{0}
, BB_{0}
и CC_{0}
треугольника ABC
пересекаются в точке H
. Окружность, проходящая через точку O
, касается стороны BC
в точке A_{0}
и при этом HA_{0}\perp BC
, поэтому A_{0}H
— диаметр окружности. Аналогично, HB_{0}
и HC_{0}
— диаметры остальных окружностей.
Пусть окружности с диаметрами HA_{0}
и HB_{0}
пересекаются в точке C_{1}
. Тогда из точки C_{1}
эти диаметры видны под прямым углом, поэтому точка C_{1}
лежит на отрезке A_{0}B_{0}
. Аналогично, точка A_{1}
пересечения окружностей с диаметрами HB_{0}
и HC_{0}
лежит на отрезке B_{0}C_{0}
, а точка B_{1}
пересечения окружностей с диаметрами HA_{0}
и HC_{0}
— на отрезке A_{0}C_{0}
.
Вершины треугольника A_{0}B_{0}C_{0}
— основания высот остроугольного треугольника ABC
, поэтому A_{0}A
, B_{0}B
и C_{0}C
— биссектрисы углов треугольника A_{0}B_{0}C_{0}
(ортотреугольника треугольника ABC
, (см. задачу 533).
При симметрии относительно прямой AA_{0}
окружность с диаметром A_{0}H
переходит в себя, а луч A_{0}C_{1}
— в луч A_{0}B_{1}
, поэтому точки B_{1}
и C_{1}
симметричны относительно прямой AA_{0}
, значит, B_{1}C_{1}\perp AA_{0}
, а так как AA_{0}\perp BC
, то B_{1}C_{1}\parallel BC
. Аналогично, A_{1}B_{1}\parallel AB
и A_{1}C_{1}\parallel AC
. Следовательно, треугольник A_{1}B_{1}C_{1}
подобен треугольнику ABC
. Что и требовалось доказать.