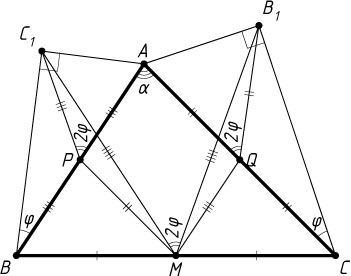
4185. На сторонах AB
и AC
треугольника ABC
внешним образом построены прямоугольные треугольники ABC_{1}
и AB_{1}C
, причём \angle C_{1}=\angle B_{1}=90^{\circ}
, \angle ABC_{1}=\angle ACB_{1}=\varphi
; M
— середина BC
. Докажите, что MB_{1}=MC_{1}
и \angle B_{1}MC_{1}=2\varphi
.
Решение. Пусть P
и Q
— середины сторон AB
и AC
соответственно. Тогда APMQ
— параллелограмм. Докажем, что треугольники MQB_{1}
и C_{1}PM
равны.
Действительно, B_{1}Q
и C_{1}P
— медианы прямоугольных треугольников AB_{1}C
и ABC_{1}
, поэтому (см. задачу 1109)
B_{1}Q=\frac{1}{2}AC=AQ=PM,~MQ=AP=\frac{1}{2}AB=C_{1}P,
\angle MQB_{1}=\angle MQA+\angle AQB_{1}=\angle MQA+2\varphi,~
\angle C_{1}PM=\angle APM+\angle APC_{1}=\angle APM+2\varphi=\angle MQA+2\varphi=\angle MQB_{1}.
Значит, треугольники MQB_{1}
и C_{1}PM
равны по двум сторонам и углу между ними. Следовательно, MB_{1}=MC_{1}
.
Обозначим \angle BAC=\alpha
. Тогда
\angle B_{1}MC_{1}=\angle PMQ-(\angle QMB_{1}+\angle PMC_{1})=\alpha-(\angle QMB_{1}+\angle MB_{1}Q)=
=\alpha-(180^{\circ}-\angle MQB_{1})=\alpha-180^{\circ}+\angle MQB_{1}=\alpha-180^{\circ}+(180^{\circ}-\alpha+2\varphi)=2\varphi.
(Случай, когда \angle C_{1}PB+\angle BPM\gt180^{\circ}
, разбирается аналогично.)