4562. Прямоугольный треугольник с острым углом \alpha
расположен внутри окружности радиуса r
так, что гипотенуза треугольника является хордой окружности, а вершина прямого угла треугольника лежит на диаметре, параллельном гипотенузе. Найдите площадь этого треугольника.
Ответ. \frac{r^{2}\sin2\alpha}{1+\sin^{2}2\alpha}
.
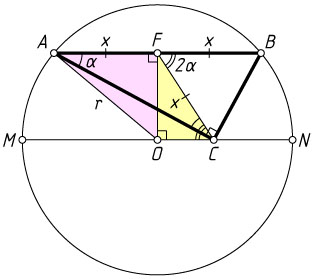
Решение. Первый способ. Пусть вершина прямого угла C
треугольника ABC
лежит на диаметре окружности с центром O
, параллельном гипотенузе AB
, \angle BAC=\alpha
. Пусть \alpha\leqslant45^{\circ}
Опустим перпендикуляр OF
из центра окружности на хорду AB
. Тогда F
— середина гипотенузы AB
. Обозначим CF=AF=BF=x
(см. задачу 1109). По теореме о внешнем угле треугольника \angle BFC=2\alpha
, поэтому \angle FCO=2\alpha
.
Из прямоугольных треугольников FOC
и FOA
находим, что
OF=FC\sin2\alpha=x\sin2\alpha,~OA^{2}=OF^{2}+AF^{2},~r^{2}=x^{2}\sin^{2}2\alpha+x^{2},
откуда x^{2}=\frac{r^{2}}{1+\sin^{2}2\alpha}
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot OF=\frac{1}{2}\cdot2x\cdot x\sin2\alpha=x^{2}\sin2\alpha=\frac{r^{2}\sin2\alpha}{1+\sin^{2}2\alpha}.
Аналогично для \alpha\gt45^{\circ}
.
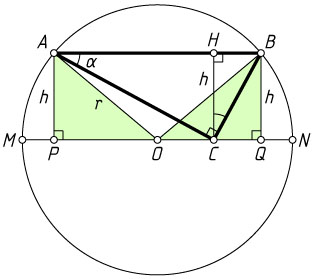
Второй способ. Пусть вершина прямого угла C
треугольника ABC
лежит на диаметре MN
, параллельном гипотенузе AB
; P
и Q
— проекции точек соответственно A
и B
на MN
; \angle CAB=\alpha
; O
— центр окружности. Обозначим высоту CH
треугольника ABC
через h
. Тогда
PQ=AB=AH+HB=h\ctg\alpha+h\tg\alpha=\frac{2h}{\sin2\alpha}.
Из прямоугольных треугольников APO
и BQO
находим, что
OP=OQ=\sqrt{r^{2}-h^{2}}.
Поэтому PQ=2\sqrt{r^{2}-h^{2}}
. Из уравнения
\frac{2h}{\sin2\alpha}=2\sqrt{r^{2}-h^{2}}
находим, что
h^{2}=\frac{r^{2}\sin^{2}2\alpha}{1+\sin^{2}2\alpha}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot CH=\frac{h^{2}}{\sin2\alpha}=\frac{r^{2}\sin2\alpha}{1+\sin^{2}2\alpha}.