4603. Круг вписан в круговой сектор с углом 2\alpha
. Найдите отношение площади сектора к площади круга.
Ответ. \frac{\alpha(1+\sin\alpha)^{2}}{\pi\sin^{2}\alpha}
.
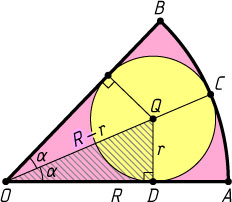
Решение. Пусть AOB
— круговой сектор круга радиуса R
с центром O
и площадью S_{1}
, Q
— центр круга радиуса r
и с площадью S_{2}
, вписанного в сектор, C
и D
— точки касания этого круга с исходной окружностью и её радиусом OA
соответственно.
Центр вписанной в угол окружности лежит на биссектрисе этого угла, поэтому \angle DOQ=\frac{1}{2}\angle AOB=\alpha
. Линия центров двух касающихся окружностей проходит через точку их касания, поэтому точки O
, Q
и C
лежат на одной прямой, значит, OQ=OC-QC=R-r
.
Из прямоугольного треугольника DOQ
находим, что QD=OQ\sin\angle DOQ
, или r=R-r\sin\alpha
, откуда r=\frac{R\sin\alpha}{1+\sin\alpha}
. Следовательно,
\frac{S_{1}}{S_{2}}=\frac{\frac{1}{2}R^{2}\cdot2\alpha}{\pi r^{2}}=\frac{R^{2}\alpha}{\pi\left(\frac{R\sin\alpha}{1+\sin\alpha}\right)^{2}}=\frac{\alpha(1+\sin\alpha)^{2}}{\pi\sin^{2}\alpha}.