4740. Радиус окружности, описанной около треугольника KLM
, равен R
. Через вершину L
проведена прямая, перпендикулярная стороне KM
. Эту прямую пересекают в точках A
и B
серединные перпендикуляры к сторонам KL
и LM
. Известно, то AL=a
. Найдите BL
.
Ответ. \frac{R^{2}}{a}
.
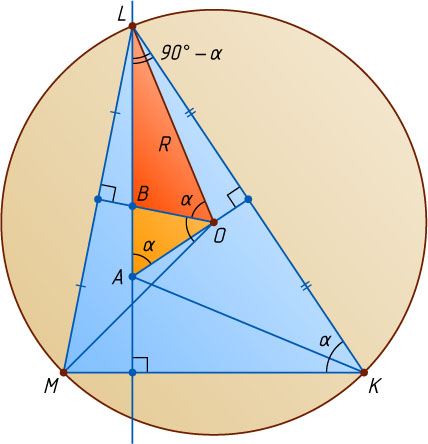
Решение. Рассмотрим случай, когда треугольник KLM
остроугольный. Пусть O
— центр его описанной окружности. Обозначим \angle LKM=\alpha
. Тогда \angle MOL=2\alpha
как центральный угол, соответствующий вписанному углу LKM
, а \angle LOB=\frac{1}{2}\angle MOL=\alpha
.
С другой стороны
\angle OAL=90^{\circ}-\angle ALK=90^{\circ}-(90^{\circ}-\alpha)=\alpha,
поэтому треугольники OAL
и BOL
подобны по двум углам, значит, \frac{BL}{OL}=\frac{OL}{AL}
, следовательно, BL=\frac{OL^{2}}{AL}=\frac{R^{2}}{a}
.
Аналогично для тупоугольного треугольника.