4782. Основание каждой высоты треугольника проецируется на боковые стороны треугольника. Докажите, что шесть полученных точек лежат на одной окружности.
Указание. Докажите сначала, что четыре из указанных проекций, лежащие на двух сторонах треугольника, образуют вписанный четырёхугольник, а затем — что каждая из двух оставшихся проекций лежит на описанной окружности этого четырёхугольника.
Решение. Рассмотрим случай остроугольного треугольника. Пусть B_{2}
и C_{2}
— проекции основания A_{1}
высоты AA_{1}
на стороны AC
и AB
треугольника ABC
. Аналогично определяются проекции C_{3}
, A_{2}
и B_{3}
, A_{3}
оснований B_{1}
и C_{1}
высот BB_{1}
и CC_{1}
(см. рис.).
Докажем сначала, что точки B_{2}
, B_{3}
, C_{2}
и C_{3}
лежат на одной окружности. Обозначим \angle ACB=\gamma
. Точки B_{1}
и C_{1}
лежат на окружности с диаметром BC
. Поэтому
\angle B_{1}C_{1}A=\angle ACB=\gamma.
Точки B_{3}
и C_{3}
лежат на окружности с диаметром B_{1}C_{1}
. Поэтому
\angle C_{3}B_{3}A=\angle B_{1}C_{1}A=\gamma.
Точки A
, C_{2}
, A_{1}
и B_{2}
лежат на одной окружности. Поэтому
\angle AC_{2}B_{2}=\angle AA_{1}B_{2}=\angle ACB=\gamma.
Следовательно,
\angle B_{2}B_{3}C_{3}+\angle C_{3}C_{2}B_{2}=(180^{\circ}-\gamma)+\gamma=180^{\circ}.
Значит, четырёхугольник B_{2}B_{3}C_{3}C_{2}
— вписанный.
Из аналогичных рассуждений следует, что \angle CA_{2}B_{2}=\angle CBA
. Поэтому A_{2}B_{2}\parallel BA
. Значит,
\angle B_{2}A_{2}C_{3}=\angle BB_{1}A_{2}=\angle ACB=\gamma=\angle B_{2}C_{2}C_{3}.
Следовательно, точка A_{2}
лежит на описанной окружности четырёхугольника B_{2}B_{3}C_{3}C_{2}
. Аналогично для точки A_{3}
.
Аналогично для любого другого треугольника.
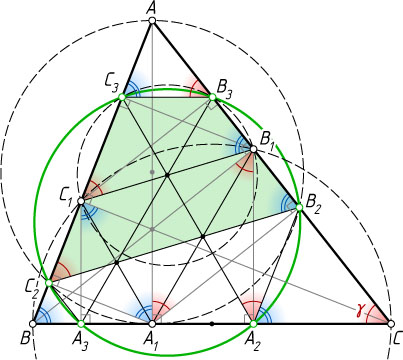
Примечание. Эта окружность называется окружностью Тэйлора (подробнее см. Дмитрий Ефремов «Новая геометрия треугольника»).
