4853. В данный сегмент вписываются всевозможные пары касающихся окружностей (см.рис.). Для каждой пары окружностей через точку касания проводится касающаяся их прямая. Докажите, что все эти прямые проходят через одну точку.
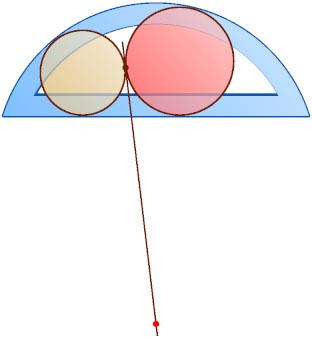
Указание. Докажите, что каждая такая касательная проходит через середину дуги, дополняющей дугу данного сегмента до окружности.
Решение. Пусть окружности S_{1}
и S_{2}
радиусов r_{1}
и r_{2}
, вписанные в сегмент окружности S
радиуса R
, касаются между собой внешним образом в точке P
, касаются хорды AB
, а также дуги AB
окружности S
в точках C
и D
соответственно. Докажем, что общая касательная к окружностям S_{1}
и S_{2}
, проведённая через точку P
, проходит через середину M
дуги AB
, не содержащей точек C
и D
.
При гомотетии с центром в точке C
и с коэффициентом \frac{R}{r_{1}}
окружность S_{1}
переходит в окружность S
, прямая AB
— в прямую l
, параллельную AB
и касающуюся окружности S
в точке M
— середине дуги AB
, не содержащей точек C
и D
. Следовательно, точка E
касания окружности S_{1}
с прямой AB
лежит на прямой CM
. Аналогично докажем, что точка F
касания окружности S_{2}
с прямой AB
лежит на прямой DM
.
Пусть MN
— диаметр окружности S
, K
— его точка пересечения с хордой AB
. Прямоугольные треугольники MKE
и MCN
подобны. Поэтому
\frac{ME}{MN}=\frac{MK}{MC},~\mbox{или}~ME\cdot MC=MK\cdot MN.
Аналогично MF\cdot MD=MK\cdot MN
. Следовательно, ME\cdot MC=MF\cdot MD
.
Докажем теперь, что прямая MP
— общая касательная к окружностям S_{1}
и S_{2}
. Предположим, что эта прямая вторично пересекает окружность S_{1}
в точке P_{1}
, а окружность S_{2}
— в точке P_{2}
. Тогда
MP_{1}\cdot MP=ME\cdot MC=MF\cdot MD=MP_{2}\cdot MP.
Поэтому точки P_{1}
и P_{2}
совпадают, а так как P
— единственная общая точка окружностей S_{1}
и S_{2}
, то точки P_{1}
и P_{2}
совпадают с точкой P
. Следовательно, MP
— общая касательная к окружностям S_{1}
и S_{2}
.
