4895. Окружности радиусов x
и y
касаются окружности радиуса R
, причём расстояние между точками касания равно a
. Вычислите длину следующей общей касательной к первым двум окружностям:
а) внешней, если оба касания внешние или внутренние одновременно;
б) внутренней, если одно касание внутреннее, а другое внешнее.
Ответ. а) \frac{a}{R}\sqrt{(R+x)(R+y)}
, \frac{a}{R}\sqrt{(R-x)(R-y)}
;
б) \frac{a}{R}\sqrt{(R+x)(R-y)}
, \frac{a}{R}\sqrt{(R+y)(R-x)}
.
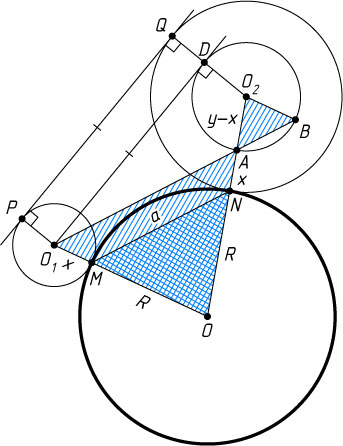
Решение. Пусть окружности радиусов x
и y
с центрами O_{1}
и O_{2}
соответственно обе касаются внешним образом в точках M
и N
окружности радиуса R
с центром O
, MN=a
.
Предположим, что x\lt y
. Рассмотрим окружность с центром O_{2}
радиуса y-x
. Пусть прямая, проходящая через точку O_{1}
параллельно MN
, пересекает эту окружность в точках A
и B
(A
между O_{1}
и B
). Тогда
AN=O_{2}N-O_{2}A=y-(y-x)=x.
Из подобия равнобедренных треугольников AOO_{1}
и NOM
находим, что
AO_{1}=MN\cdot\frac{OA}{ON}=a\cdot\frac{R+x}{R},
а из подобия равнобедренных треугольников ABO_{2}
и AO_{1}O
—
AB=AO_{1}\cdot\frac{O_{2}A}{OA}=\frac{a(R+x)}{R}\cdot\frac{y-x}{R+x}=\frac{a(y-x)}{R}.
Поэтому
O_{1}B=AO_{1}+AB=\frac{a(R+x)}{R}+\frac{a(y-x)}{R}=\frac{a(R+y)}{R}.
Пусть PQ
— общая внешняя касательная окружностей радиусов x
и y
(точка P
на первой окружности, Q
— на второй). Тогда прямая, проведённая через точку O_{1}
параллельно PQ
, касается окружности радиуса y-x
с центром O_{2}
в некоторой точке D
, и PQ=O_{1}D
. По теореме о касательной и секущей
PQ^{2}=O_{1}D^{2}=O_{1}B\cdot O_{1}A=\frac{a(R+y)}{R}\cdot\frac{a(R+x)}{R}=\left(\frac{a}{R}\right)^{2}\cdot(R+y)(R+x).
Следовательно, PQ=\frac{a}{R}\sqrt{(R+x)(R+y)}
.
Если окружности радиусов x
и y
обе касаются окружности радиуса R
внутренним образом, то аналогично получим, что PQ=\frac{a}{R}\sqrt{(R-x)(R-y)}
.
Если же одна из меньших окружностей касается большей внешним образом, а вторая — внутренним, то, построив окружность с центром O_{2}
радиуса y+x
, аналогично получим, что PQ=\frac{a}{R}\sqrt{(R+x)(R-y)}
или PQ=\frac{a}{R}\sqrt{(R+y)(R-x)}
.