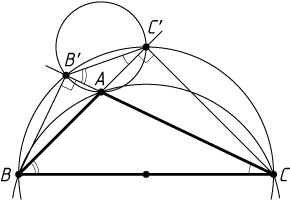
4965. Около треугольника ABC
с высотами BB'
и CC'
описана окружность радиуса 6. Найдите радиусы окружностей, описанных около треугольников BB'C
и AB'C'
, если \cos A=-\frac{1}{3}
.
Ответ. 4\sqrt{2}
, 2.
Решение. Заметим, что \angle BAC\gt90^{\circ}
. Пусть радиус описанной около треугольника ABC
окружности равен R
. По теореме синусов
BC=2R\sin A=2R\sqrt{1-\cos^{2}A}=2\cdot6\cdot\sqrt{1-\frac{1}{9}}=8\sqrt{2}.
Радиус R_{1}
окружности, окружности около прямоугольного треугольника BB'C
равен половине гипотенузы BC
,т. е.
R_{1}=\frac{1}{2}BC=4\sqrt{2}.
Из точек B'
и C'
сторона BC
видна под прямым углом, значит, эти точки лежат на окружности с диаметром BC
. Вписанные в эту окружность углы BC'B'
и BCB'
опираются на одну и ту же дугу, поэтому они \angle BC'B'=\angle BCB'
. Аналогично, \angle CB'C'=\angle CBB'
, поэтому, треугольник AB'C'
подобен треугольнику ABC
, причём коэффициент подобия равен отношению соответствующих сторон, т. е.
k=\frac{AC'}{AC}=\cos\angle CAC'=\cos(180^{\circ}-\angle BAC)=-\cos\angle BAC=\frac{1}{3}.
Следовательно, если R_{2}
— радиус окружности, описанной около треугольника AB'C'
, то
R_{2}=kR=\frac{1}{3}\cdot6=2.