5092. Расстояние от точки P
до центра окружности радиуса R
, описанной около треугольника ABC
, равно d
. Точки K
, M
и N
— основания перпендикуляров, опущенных из точки P
на прямые BC
, AC
и AB
соответственно. Докажите, что отношение площадей треугольников KMN
и ABC
равно \frac{|R^{2}-d^{2}|}{4R^{2}}
.
Решение. Обозначим через \alpha
и \beta
углы при вершинах соответственно A
и B
треугольника ABC
. Рассмотрим случай, когда точка P
лежит внутри описанной окружности \Omega
треугольника ABC
. Пусть луч AP
пересекает окружность \Omega
в точке D
. Тогда AP\cdot PD=R^{2}-d^{2}
(см. задачу 2635).
Пусть X
и Y
— проекции точки P
на прямые BD
и CD
соответственно. Из точек X
и Y
отрезок PD
виден под прямым углом, значит, эти точки лежат на окружности с диаметром PD
. Обозначим её \omega
. Аналогично точки N
, X
и K
лежат на окружности с диаметром PB
(обозначим её \omega_{1}
), а точки M
и N
лежат на окружности с диаметром AP
(обозначим её \omega_{2}
).
Вписанные в окружность \omega
углы PDY
и PXY
опираются на одну и ту же дугу, поэтому
\angle PXY=\angle PDY=\angle ADC=\angle ABC.
Аналогично \angle PYX=\angle ACB
. Следовательно, треугольник PXY
подобен треугольнику ABC
по двум углам.
Вписанные в окружность \omega_{1}
углы PNK
и PBK
опираются на одну и ту же дугу, поэтому \angle PNK=\angle PBK
. Вписанные в окружность \omega_{2}
углы PNM
и PAM
также опираются на одну и ту же дугу, поэтому
\angle PNM=\angle PAM=\angle DAC=\angle DBC=\angle XBK.
Значит, либо
\angle PBX=\angle PBK+\angle XBK=\angle PNK+\angle PNM=\angle MNK
(см. рис. 1), либо
\angle PBX=\angle XBK-\angle PBK=\angle PNM-\angle PNK=\angle MNK
(см. рис. 2).
Из прямоугольного треугольника PBX
получаем, что
PX=BP\sin\angle PBX=BP\sin\angle MNK.
Пусть PH
и AT
— высоты треугольников PXY
и ABC
, а KE
— высота треугольника KMN
. Тогда
PH=PX\sin\angle PXY=PX\sin\beta=BP\sin\angle MNK\sin\beta=
=PB\sin\beta\sin\angle MNK=NK\sin\angle MNK=KE,
поэтому
\frac{PD}{2R}=\frac{PH}{AT}=\frac{KE}{AT}.
В то же время, выражая \sin\alpha
по теореме синусов из треугольников AMN
и ABC
, получим, что \frac{MN}{AP}=\frac{BC}{2R}
, или \frac{AP}{2R}=\frac{MN}{BC}
. Тогда
\frac{AP}{2R}\cdot\frac{PD}{2R}=\frac{MN}{BC}\cdot\frac{KE}{AT}=\frac{MN\cdot KE}{BC\cdot AT}=\frac{2S_{\triangle KMN}}{2S_{\triangle ABC}}=\frac{S_{\triangle KMN}}{S_{\triangle ABC}}.
С другой стороны, AP\cdot PD=R^{2}-d^{2}
, поэтому
\frac{AP}{2R}\cdot\frac{PD}{2R}=\frac{AP\cdot PD}{4R^{2}}=\frac{R^{2}-d^{2}}{4R^{2}}.
Следовательно,
\frac{S_{\triangle KMN}}{S_{\triangle ABC}}=\frac{R^{2}-d^{2}}{4R^{2}}.
Если точка P
лежит вне окружности \Omega
, то аналогично
\frac{S_{\triangle KMN}}{S_{\triangle ABC}}=\frac{d^{2}-R^{2}}{4R^{2}}.
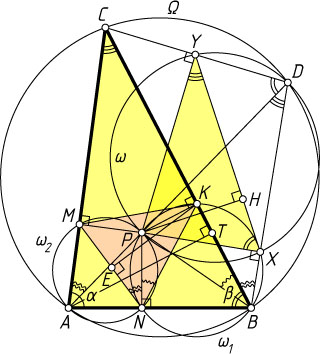
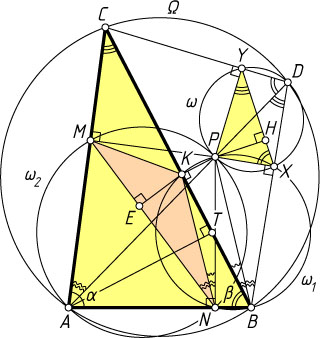
Примечание. 1. Для данного треугольника ABC
площади S
площадь треугольника KMN
(педального, или подерного треугольника) однозначно определяется расстоянием d
от точки P
до центра O
описанной окружности треугольника ABC
:
S_{\triangle KMN}=\frac{|d^{2}-R^{2}|}{4R^{2}}S=\frac{1}{4}\left|1-\frac{d^{2}}{R^{2}}\right|S.
Если d=0
(точка P
совпадает с O
), то S_{\triangle KMN}=\frac{1}{4}S
. В этом случае вершины треугольника KMN
— середины сторон треугольника ABC
.
Если d=R
, то точки K
, M
и N
лежат на одной прямой — прямой Симсона треугольника ABC
и точки P
(см. задачи 83 и 6088).
Если 0\lt d\lt R\sqrt{2}
, то S_{\triangle KMN}\lt\frac{1}{4}S
.
Если d\gt R\sqrt{2}
, то S_{\triangle KMN}\gt\frac{1}{4}S
.
Обратные утверждения также верны.
Геометрическое место точек P
, для которых треугольники KMN
равновелики и их площади меньше \frac{1}{4}S
, есть две окружности, концентрические описанной окружности треугольника ABC
. Если же их площадь больше \frac{1}{4}S
, то указанное геометрическое место — одна такая окружность.
В первом из этих случаев, если d_{1}
и d_{2}
— радиусы этих окружностей, то
\frac{1}{4}\left|1-\frac{d_{1}^{2}}{R^{2}}\right|S=\frac{1}{4}\left|1-\frac{d_{2}^{2}}{R^{2}}\right|S~\Leftrightarrow~d_{1}=d_{2}~\mbox{или}~d_{1}^{2}+d_{2}^{2}=2R^{2}.
2. См. также статью И.А.Кушнира «О двух формулах Эйлера», Квант, 1992, N12, с.43-46.

