5133. С помощью циркуля и линейки впишите в данную окружность n
-угольник, стороны которого соответственно параллельны n
данным прямым.
Указание. Проведите через центр окружности n
прямых, перпендикулярных данным, и рассмотрите композицию n
симметрий относительно этих прямых. Разберите отдельно случаи чётного и нечётного n
.
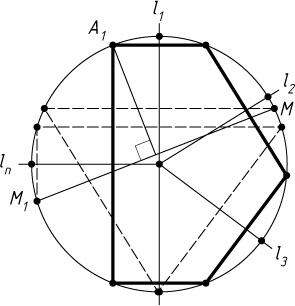
Решение. Проведём через центр окружности n
прямых l_{1}
, l_{2}
, \ldots
, l_{n}
, соответственно перпендикулярных данным. Тогда эти прямые будут серединными перпендикулярами к сторонам A_{1}A_{2}
, A_{2}A_{3}
, \ldots
, A_{n}A_{1}
искомого n
-угольника.
При композиции n
симметрий относительно прямых l_{1}
, l_{2}
, \ldots
, l_{n}
вершина A_{1}
переходит в себя. Пусть n
— нечётное число (рис. 1). Тогда рассматриваемая композиция есть симметрия относительно некоторой прямой l
, проходящей через вершину A_{1}
.
Отсюда вытекает следующий способ построения. Строим образ M_{1}
произвольной точки M
данной окружности при композиции симметрий относительно прямых l_{1}
, l_{2}
, \ldots
, l_{n}
, соответственно перпендикулярных данным n
прямым. Пересечение серединного перпендикуляра к отрезку MM_{1}
с данной окружностью есть вершина A_{1}
искомого n
-угольника. Остальные вершины строятся с помощью симметрий относительно прямых l_{1}
, l_{2}
, \ldots
, l_{n-1}
. Задача имеет два решения.
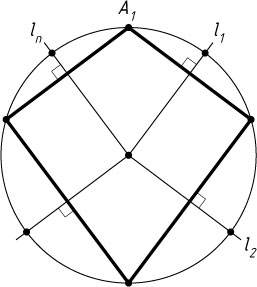
Пусть n
— чётное число (рис. 2). Тогда рассматриваемая композиция представляет собой поворот вокруг центра данной окружности. Из того, что точка A_{1}
при этом преобразовании переходит в себя, следует, что это поворот на угол, кратный 360^{\circ}
, т. е. тождественное преобразование.
В этом случае задача имеет бесконечное множество решений. В качестве вершины A_{1}
можно взять любую точку окружности, не лежащую ни на одной из прямых l_{1}
, l_{2}
, \ldots
, l_{n}
. Это возможно только в случае, когда сумма углов \alpha_{1}
, \alpha_{3}
, \ldots
, \alpha_{n-1}
кратна 180^{\circ}
(\alpha_{1}
— угол между прямыми l_{1}
и l_{2}
, \alpha_{3}
— между l_{3}
и l_{4}
и т. д.).
Если это не так, то задача не имеет решений.