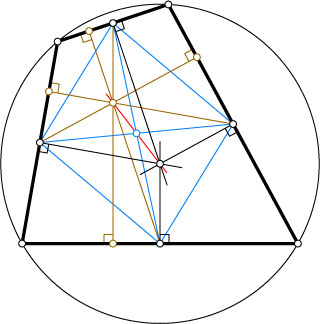
5706. Теорема Монжа. Докажите, что прямые, проведённые через середины сторон вписанного четырёхугольника перпендикулярно противоположным сторонам, пересекаются в одной точке (точке Монжа вписанного четырёхугольника).
Указание. Середины сторон любого четырёхугольника являются вершинами параллелограмма (см. задачу 1204).
Решение. Середины сторон четырёхугольника являются вершинами параллелограмма (см. задачу 1204). При симметрии относительно точки пересечения диагоналей этого параллелограмма рассматриваемые перпендикуляры переходят в серединные перпендикуляры к сторонам данного четырёхугольника. Поскольку данный четырёхугольник вписанный, то эти серединные перпендикуляры пересекаются в одной точке — центре описанной окружности. Следовательно, рассматриваемые перпендикуляры также пересекаются в одной точке.
(Из задачи 1223 следует, что в этой же точке пересекаются и перпендикуляры, опущенные из середины одной диагонали на другую.)

Примечание. Верно и обратное: если перпендикуляры к сторонам выпуклого четырёхугольника, проведённые через середины противоположных сторон, пересекаются в одной точке, то четырёхугольник вписанный.
Действительно, пусть
ABCD
— выпуклый четырёхугольник,
K
,
L
,
M
и
N
— середины сторон соответственно
AB
,
BC
,
CD
и
AD
, а
k
,
l
,
m
и
n
— перпендикуляры, опущенные из точек
K
,
L
,
M
и
N
на стороны
CD
,
AD
,
AB
и
BC
соответственно. Тогда
KLMN
— параллелограмм (см. задачу 1204), а при симметрии относительно общей середины
O
его диагоналей перпендикуляры
k
,
l
,
m
и
n
переходят в серединные перпендикуляры к сторонам соответственно
CD
,
AD
,
AB
и
BC
. Значит, если перпендикуляры
k
,
l
,
m
и
n
пересекаются в одной точке, то в одной точке пересекаются и серединные перпендикуляры к сторонам четырёхугольника
ABCD
. Следовательно, около него можно описать окружность.
2.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 16.4, с. 48
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 16.4, с. 354
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 21.33, с. 198