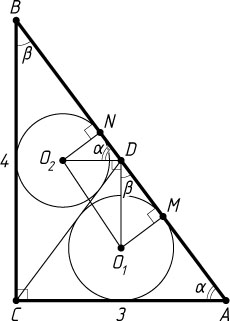
5779. В прямоугольном треугольнике ABC
из вершины прямого угла C
проведена медиана CD
. Найдите расстояние между центрами окружностей, вписанных в треугольники ACD
и BCD
, если BC=4
, а радиус окружности, описанной около треугольника ABC
, равен \frac{5}{2}
.
Ответ. \frac{5\sqrt{13}}{12}
.
Решение. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы, поэтому AB=2\cdot\frac{5}{2}=5
. По теореме Пифагора
AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{25-16}=3.
Обозначим \angle BAC=\alpha
, \angle ABC=\beta
. Тогда
\sin\alpha=\frac{BC}{AB}=\frac{4}{5},~\sin\beta=\frac{AC}{AB}=\frac{3}{5}.
Пусть O_{1}
и O_{2}
— центры окружностей, вписанных в треугольники ACD
и BCD
соответственно, а M
и N
— точки касания этих окружностей со стороной AB
. Отрезки O_{1}M
и O_{2}N
— радиусы вписанных окружностей треугольников ADC
и BDC
, поэтому
O_{1}M=\frac{2S_{\triangle ADC}}{AC+AD+CD}=\frac{S_{\triangle ABC}}{AC+AD+CD}=\frac{\frac{1}{2}\cdot3\cdot4}{3+\frac{5}{2}+\frac{5}{2}}=\frac{6}{8}=\frac{3}{4},
O_{2}N=\frac{2S_{\triangle BDC}}{BC+BD+CD}=\frac{S_{\triangle ABC}}{BC+BD+CD}=\frac{\frac{1}{2}\cdot3\cdot4}{4+\frac{5}{2}+\frac{5}{2}}=\frac{6}{9}=\frac{2}{3}.
Угол BDC
— внешний угол равнобедренного треугольника ACD
(AD=CD=\frac{5}{2}
), поэтому \angle BDC=2\alpha
, а так как DO_{2}
— биссектриса этого угла, то \angle NDO_{2}=\alpha
. Аналогично \angle MDO_{1}=\beta
.
Из прямоугольных треугольников NDO_{2}
и MDO_{1}
находим, что
DO_{2}=\frac{O_{2}N}{\sin\alpha}=\frac{\frac{2}{3}}{\frac{4}{5}}=\frac{5}{6},~DO_{1}=\frac{O_{1}M}{\sin\beta}=\frac{\frac{3}{4}}{\frac{3}{5}}=\frac{5}{4}.
Поскольку \angle O_{1}DO_{2}=90^{\circ}
как угол между биссектрисами смежных углов,
O_{1}O_{2}=\sqrt{DO_{1}^{2}+DO_{2}^{2}}=\sqrt{\frac{25}{16}+\frac{25}{36}}=\frac{5\sqrt{13}}{12}.