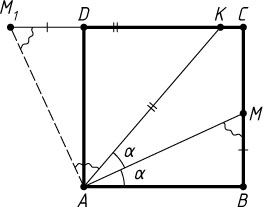
6005. На сторонах BC
и CD
квадрата ABCD
взяты точки M
и K
соответственно, причём \angle BAM=\angle MAK
. Докажите, что BM+KD=AK
.
Указание. Поверните квадрат ABCD
относительно вершины A
на 90^{\circ}
так, чтобы вершина B
перешла в вершину D
.
Решение. Повернём квадрат ABCD
относительно вершины A
на 90^{\circ}
так, чтобы вершина B
перешла в вершину D
. Тогда точка M
перейдёт в точку M_{1}
, лежащую на продолжении стороны CD
за точку D
, и M_{1}D=BM
.
Обозначим \angle BAM=\angle MAK=\alpha
. Тогда
\angle MAM_{1}=90^{\circ},~\angle AM_{1}K=\angle AM_{1}D=\angle AMB=90^{\circ}-\alpha,
\angle M_{1}AK=\angle MAM_{1}-\angle MAK=90^{\circ}-\alpha=\angle AM_{1}K.
Значит, треугольник AKM_{1}
— равнобедренный. Следовательно,
AK=KM_{1}=KD+DM_{1}=KD+BM.