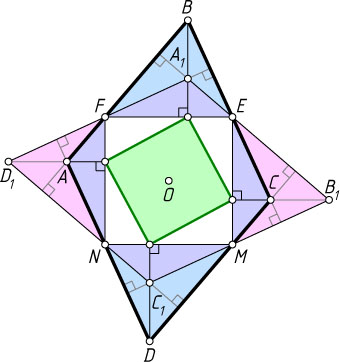
6036. Вокруг квадрата описан параллелограмм (вершины квадрата лежат на разных сторонах параллелограмма). Докажите, что перпендикуляры, опущенные из вершин параллелограмма на стороны квадрата, образуют новый квадрат.
Указание. Докажите, что указанные перпендикуляры переходят друг в друга при повороте на 90^{\circ}
вокруг центра вписанного в параллелограмм квадрата.
Решение. Пусть вершины F
, E
, M
и N
квадрата FEMN
лежат на сторонах соответственно AB
, BC
, CD
и AD
параллелограмма ABCD
. Достаточно доказать, что при повороте на 90^{\circ}
вокруг общего центра O
квадрата FEMN
и параллелограмма ABCD
(см. задачу 1057) указанные перпендикуляры переходят друг в друга.
Пусть параллелограмм A_{1}B_{1}C_{1}D_{1}
— образ параллелограмма ABCD
при этом повороте (точка A_{1}
— образ точки A
и т. д.). Поскольку стороны параллелограмма A_{1}B_{1}C_{1}D_{1}
перпендикулярны сторонам параллелограмма ABCD
, то FA_{1}\perp BC
и A_{1}E\perp AB
. Поэтому A_{1}
— точка пересечения высот треугольника BEF
и, следовательно, BA_{1}\perp EF
. Значит, перпендикуляр, опущенный из вершины A
на сторону NF
квадрата FEMN
, переходит при рассматриваемом повороте в перпендикуляр, опущенный из вершины B
на сторону FE
. Отсюда следует утверждение задачи.