6065. Диаметр вписанной окружности треугольника ABC
, проходящий через точку касания со стороной BC
, пересекает хорду, соединяющую две другие точки касания, в точке N
. Докажите, что прямая AN
делит сторону BC
пополам.
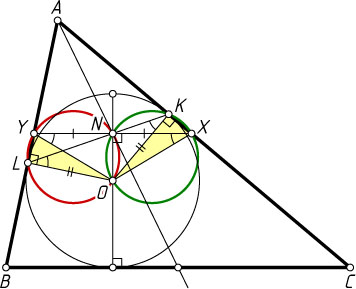
Решение. Первый способ. Пусть вписанная окружность с центром O
треугольника ABC
касается сторон AC
и AB
в точках K
и L
соответственно, а прямая, проведённая через точку N
параллельно BC
, пересекает стороны AC
и AB
в точках соответственно X
и Y
. Предположим, что точка K
лежит между A
и X
.
Из точек K
и N
отрезок OX
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OX
. Вписанные в эту окружность углы OXN
и OKN
опираются на одну и ту же дугу, поэтому \angle OXN=\angle OKN=\angle OKL
. Аналогично \angle OYN=\angle OLK
, а так как OK=OL
, то \angle OKL=\angle OLK
, поэтому \angle OXN=\angle OYN
. Значит, N
— середина основания XY
равнобедренного треугольника OXY
, а так как XY\parallel BC
, то прямая AN
проходит через середину стороны BC
(см. задачу 2607). Что и требовалось доказать.
Второй способ. Заметим, что точки K
, L
и N
— проекции точки O
на прямые, содержащие стороны треугольника AXY
. Поскольку точки K
, L
и N
лежат на одной прямой, точка O
лежит на описанной окружности треугольника AXY
(см. задачу 6088). Луч AO
— биссектриса угла A
, поэтому O
— середина дуги XOY
. Значит, N
— середина XY
(ON
— высота равнобедренного треугольника XOY
), а так как XY\parallel BC
, то прямая AN
проходит через середину стороны BC
(см. задачу 2607). Что и требовалось доказать.
Примечание. 1. См. также статью Д.Прокопенко, Д.Швецова «Вокруг точки на медиане», Квант, 2020, N2, с.42-46.
2. Верно также следующее обобщение доказанного утверждения. Если из некоторой точки T
биссектрисы угла A
треугольника ABC
опущены перпендикуляры TA_{1}
, TB_{1}
и TC_{1}
на его стороны BC
, CA
и AB
соответственно, а P
— точка пересечения прямых TA_{1}
и B_{1}C_{1}
, то прямая AP
делит сторону BC
пополам. (Доказательство аналогично изложенному выше.)
