6096. Точки A
, B
и C
лежат на одной прямой, точка P
— вне этой прямой. Докажите, что центры описанных окружностей треугольников ABP
, BCP
, ACP
и точка P
лежат на одной окружности.
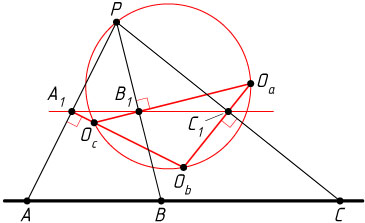
Решение. Пусть A_{1}
, B_{1}
и C_{1}
— середины отрезков AP
, BP
и CP
соответственно. Тогда центр O_{c}
описанной окружности треугольника ABP
— точка пересечения перпендикуляра к AP
, проходящего через точку A_{1}
, и перпендикуляра к BP
, проходящего через точку B_{1}
. Аналогично для центров O_{b}
и O_{a}
описанных окружностей треугольников ACP
и BCP
.
Точки A_{1}
, B_{1}
и C_{1}
— основания перпендикуляров, опущенных из точки P
на стороны треугольника O_{a}O_{b}O_{c}
или на их продолжения, а так как точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой (прямой, содержащей среднюю линию треугольника APC
), то точка P
лежит на описанной окружности треугольника O_{a}O_{b}O_{c}
(A_{1}C_{1}
— прямая Симсона, соответствующая точке P
, см. задачу 83). Что и требовалось доказать.