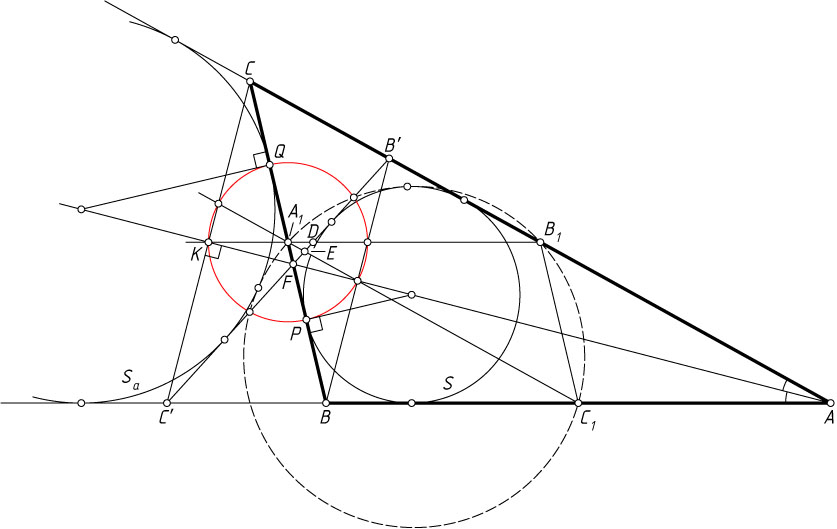
6117. Теорема Фейербаха. Докажите, что окружность, проходящая через середины трёх сторон треугольника, касается его вписанной и трёх вневписанных окружностей.
Решение. Первый способ. Пусть A_{1}
, B_{1}
и C_{1}
— середины сторон BC=a
, AC=b
и AB=c
треугольника ABC
, S
— вписанная окружность треугольника ABC
, касающаяся стороны BC
в точке P
, S_{a}
— вневписанная окружность, касающаяся стороны BC
в точке Q
, p
— полупериметр треугольника ABC
. Если b=c
, то утверждение очевидно. Рассмотрим случай, когда b\ne c
.
Тогда
CP=p-AB=p-c,~A_{1}P=|CP-CA_{1}|=\left|p-c-\frac{a}{2}\right|=\frac{|b-c|}{2}
(см. задачи 219 и 4805).
При симметрии относительно биссектрисы угла BAC
вершина B
переходит в точку B'
луча AC
, вершина C
— в точку C'
луча AB
, а окружности S
и S_{a}
переходят сами в себя. Значит, прямая B'C'
— вторая общая внутренняя касательная окружностей S
и S_{a}
.
При этом, так как треугольник ACC'
равнобедренный, биссектриса угла BAC
пересекает его основание CC'
в середине K
, точки B_{1}
, A_{1}
и K
лежат на одной прямой — средней линии треугольника ACC'
, а
A_{1}K=\frac{1}{2}B'C=\frac{1}{2}|AC'-AB|=\frac{1}{2}|AC-AB|=\frac{1}{2}|b-c|=A_{1}P.
Аналогично, A_{1}K=A_{1}Q
, поэтому A_{1}Q=A_{1}P
.
Пусть прямые BC
, A_{1}B_{1}
и A_{1}C_{1}
пересекают прямую B'C'
в точках F
, D
и E
соответственно. Треугольник A_{1}FD
подобен треугольнику BFC'
с коэффициентом \frac{A_{1}F}{FB}
, а треугольник A_{1}FK
подобен треугольнику BFA
с тем же коэффициентом, поэтому
\frac{A_{1}D}{A_{1}K}=\frac{BC'}{AB}=\frac{A_{1}K}{A_{1}B_{1}},
откуда находим, что
A_{1}D\cdot A_{1}B_{1}=A_{1}K^{2}=A_{1}P^{2}.
Аналогично, A_{1}E\cdot A_{1}C_{1}=A_{1}P^{2}
. Следовательно, при инверсии с центром A_{1}
и радиусом A_{1}P
точки B_{1}
и C_{1}
перейдут в точки D
и E
, описанная окружность треугольника A_{1}B_{1}C_{1}
, проходящая через центр инверсии, перейдёт в прямую DE
, т. е. в прямую B'C'
.
Осталось заметить, что при рассматриваемой инверсии окружности S
и S_{a}
, не проходящие через центр инверсии, переходят сами в себя. Действительно, если X'
— образ точки X
, лежащей на окружности S
, то A_{1}X'\cdot A_{1}X=A_{1}P^{2}
, значит, точка X'
также лежит на окружности S
. Аналогично для окружности S_{a}
(A_{1}Q=A_{1}P
).
Если ещё раз применить рассматриваемую инверсию, то прямая B'C'
перейдёт в описанную окружность треугольника A_{1}B_{1}C_{1}
, окружности S
и S_{a}
— сами в себя, а так как прямая B'C'
— общая касательная к окружностям S
и S_{a}
, то её образ также касается окружностей S
и S_{a}
. Что и требовалось доказать.
Второй способ. Пусть r
и R
— радиусы соответственно вписанной и описанной окружностей треугольника ABC
со сторонами BC=a
, AC=b
и AB=c
; p
— полупериметр треугольника; I
— центр вписанной окружности, O
— центр описанной окружности, E
— центр окружности, проходящей через середины сторон треугольника, H
— ортоцентр данного треугольника.
Треугольник с вершинами в серединах сторон данного треугольника подобен данному с коэффициентом \frac{1}{2}
, поэтому радиус окружности, описанной около этого треугольника равен \frac{1}{2}R
. Докажем, что эта окружность и вписанная окружность данного треугольника касаются внутренним образом. Для этого достаточно доказать, что расстояние между центрами этих окружностей равно разности их радиусов, т. е. EI=\frac{1}{2}R-r
.
Воспользуемся векторными равенствами
\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC},~\overrightarrow{OI}=\frac{1}{2p}(a\overrightarrow{OA}+b\overrightarrow{OB}+c\overrightarrow{OC})
(см. задачи 4516 и 4159). Учитывая, что точка E
— середина отрезка OH
(см. задачу 174), получим, что
\overrightarrow{EI}=\overrightarrow{OI}-\overrightarrow{OE}=\overrightarrow{OI}-\frac{1}{2}\overrightarrow{OH}=
\frac{1}{2p}(a\overrightarrow{OA}+b\overrightarrow{OB}+c\overrightarrow{OC})-\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})=
=\frac{1}{2p}((a-p)\overrightarrow{OA}+(b-p)\overrightarrow{OB}+(c-p)\overrightarrow{OC}).
Возведя в скалярный квадрат равенство \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}
, получим, что
\overrightarrow{AB}^{2}=\overrightarrow{OB}^{2}+\overrightarrow{OA}^{2}-2\overrightarrow{OB}\cdot\overrightarrow{OA},
или
c^{2}=2R^{2}-2\overrightarrow{OB}\cdot\overrightarrow{OA}.
Отсюда находим, что
2\overrightarrow{OB}\cdot\overrightarrow{OA}=2R^{2}-c^{2}.
Аналогично
2\overrightarrow{OA}\cdot\overrightarrow{OC}=2R^{2}-b^{2},~2\overrightarrow{OB}\cdot\overrightarrow{OC}=2R^{2}-a^{2}.
Значит,
\overrightarrow{EI}^{2}=\frac{1}{4p^{2}}((a-p)^{2}\overrightarrow{OA}^{2}+(b-p)^{2}\overrightarrow{OB}^{2}+(c-p)^{2}\overrightarrow{OC}^{2}+
+2(a-p)(b-p)\overrightarrow{OA}\cdot\overrightarrow{OB}+2(a-p)(c-p)\overrightarrow{OA}\cdot\overrightarrow{OC}+2(b-p)(c-p)\overrightarrow{OB}\cdot\overrightarrow{OC})=
=\frac{1}{4p^{2}}((a-p)^{2}R^{2}+(b-p)^{2}R^{2}+(c-p)^{2}R^{2}+
+(a-p)(b-p)(2R^{2}-c^{2})+(a-p)(c-p)(2R^{2}-b^{2})+(b-p)(c-p)(2R^{2}-a^{2}))=
=\frac{1}{4p^{2}}(((a-p)^{2}+(b-p)^{2}+(c-p)^{2}+2(a-p)(b-p)+2(a-p)(c-p)+2(b-p)(c-p))R^{2}-
-((b-p)(c-p)a^{2}+(a-p)(c-p)b^{2}+(b-p)(a-p)c^{2}))=
=\frac{1}{4p^{2}}(a-p+b-p+c-p)^{2}R^{2}-
-((b-p)(c-p)a^{2}+(a-p)(c-p)b^{2}+(b-p)(a-p)c^{2}))=
=\frac{1}{4p^{2}}\cdot p^{2}R^{2}-\frac{1}{4p^{2}}((b-p)(c-p)a^{2}+(a-p)(c-p)b^{2}+(b-p)(a-p)c^{2}))=
=\frac{1}{4}R^{2}-\frac{1}{4p^{2}}((b-p)(c-p)a^{2}+(a-p)(c-p)b^{2}+(b-p)(a-p)c^{2})).
Применив равенство
a^{2}(p-b)(p-c)+b^{2}(p-a)(p-c)+c^{2}(p-a)(p-b)=4p^{2}r(R-r)
(см. задачу 4127), получим, что
EI^{2}=\overrightarrow{EI}^{2}=\frac{1}{4}R^{2}-r(R-r)=\frac{1}{4}R^{2}-2rR+r^{2}=\left(\frac{1}{2}R-r\right)^{2},
а так как R\geqslant2r
(см. задачу 3587), то IE=\frac{1}{2}R-r
. Что и требовалось доказать.
Аналогично можно доказать, что каждая из вневписанных окружностей треугольника также касается окружности, проходящей через середины его сторон.